Spezielle Relativitätstheorie
Einsteins Postulate erweiterten die Galilei'sche Mechanik, Raum und Zeit wurden zur vierdimensionalen Raumzeit zusammengeführt und die Konstanten Zeit, Länge und Masse wurden neu definiert. Daraus folgen die Zeitdilatation, Längenkontraktion und relativistische Massenzunahme.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Einleitung und Historie
- Einsteins Postulate
- Zeitdilatation
- Längenkontraktion
- Minkowski Diagramme
- Relativistische Massenzunahme
- Optischer Dopplereffekt
Einleitung und Historie
Die spezielle Relativitätstheorie ist wohl eine der berühmtesten physikalischen Theorien. Veröffentlicht wurde sie 1905 von Albert Einstein und wurde in den über 100 Jahren ihres Bestehens von zahlreichen Experimenten bestätigt.

In seiner Theorie erweiterte Einstein das Galilei'sche Relativitätsprinzip um zwei entscheidende Postulate und veränderte damit das Verständnis von Raum und Zeit. In seiner Theorie stellte Einstein auch die nicht weniger berühmte Formel auf, die sogenannte Äquivalenz von Masse und Energie.
$E=mc^2$
Das Galilei'sche Relativitätsprinzip
Galileo Galilei entdeckte, dass die Gesetze der Mechanik unabhängig davon gelten, ob man sich in Ruhe befindet oder mit konstanter Geschwindigkeit (gleichförmig) fortbewegt.
Ein Beispiel
Wirfst du einen Ball in die Luft und fängst ihn wieder auf, wird der Ball derselben Flugbahn folgen, egal ob du es auf der Straße tust oder in einem fahrenden Zug. Stelle dir nun also vor, der Zug hätte keine Fenster und würde nicht beschleunigen oder bremsen. Dann könntest du nicht unterscheiden, ob er steht oder mit konstanter Geschwindigkeit fährt.

Einsteins Postulate
1. Postulat: Einstein erkannte, dass das Relativitätsprinzip nicht nur für die Mechanik gilt. Stattdessen seien alle physikalischen Gesetze in allen Inertialsystemen gleich. Außerdem gibt es kein ausgezeichnetes Inertialsystem: Raum und Zeit sind relativ und hängen vom Beobachter ab.
2. Postulat: Da das Relativitätsprinzip insbesondere auch für die Elektrodynamik gilt, folgt daraus unweigerlich, dass die Lichtgeschwindigkeit $c$ im Vakuum in jedem Inertialsystem gleich ist. Sie hat den Wert $c=299.792.458\,\frac{\text{m}}{\text{s}}$ und ist die maximal erreichbare Geschwindigkeit. Wie das Reisen mit Lichtgeschwindigkeit aussehen würde, kann man am Computer simulieren.
Zeitdilatation
in der klassischen Physik gibt es einen dreidimensionalen Raum und unabhängig davon eine absolute Zeit. In der speziellen Relativitätstheorie werden der Raum und die Zeit durch die Einstein'sche Raumzeit gemeinsam beschrieben. Raum und Zeit hängen hier von der Geschwindigkeit des Beobachters ab. Einem Beobachter erscheint die Zeit $t$ in einem relativ zu ihm bewegten Inertialsystem gedehnt. Dieses Phänomen bezeichnet man als Zeitdilatation und die Formel lautet
$t=\frac{t'}{\sqrt{1-\frac{v^2}{c^2}}}$.
Uhren in einem Flugzeug $t$ gehen also tatsächlich etwas langsamer als auf dem Erdboden $t'$.
Längenkontraktion
Einem Beobachter erscheinen Strecken $l$ kürzer, je schneller er sich bewegt. Dieses Phänomen bezeichnet man als Längenkontraktion, und die entsprechende Formel lautet
$l=l'\cdot\sqrt{1-\frac{v^2}{c^2}}$.
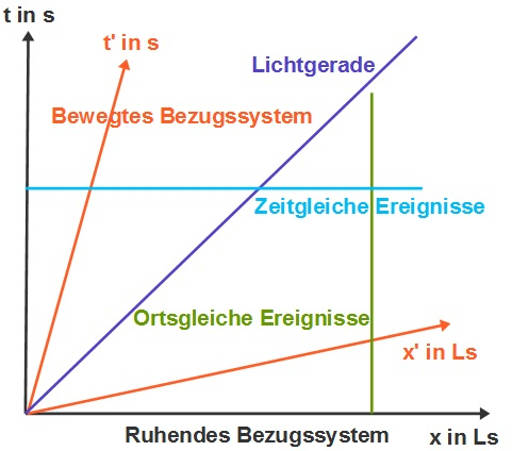
Minkowski Diagramme
Mit Hilfe von Minkowski Diagrammen lassen sich relativistische Vorgänge in zwei oder mehr Inertialsystemen korrekt darstellen. Sie sind eine Erweiterung zu klassischen, kartesischen Koordinatensystemen und gut dafür geeignet, Zeitdilatation und Längenkontraktion anschaulich darzustellen.
Relativistische Massenzunahme
Ein weiteres Phänomen der speziellen Relativitätstheorie ist die relativistische Massenzunahme. Diese besagt, dass die Masse $m$ eines Objekts mit zunehmender Geschwindigkeit wächst. Die Masse in der klassischen Physik entspricht hier der Ruhemasse $m_0$. Die Formel lautet
$m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$.
Die relativistische Massenzunahme ist auch ein Grund, warum es für Objekte mit Masse unmöglich ist, die Lichtgeschwindigkeit zu erreichen. Da die Masse des Objekts immer größer wird, je schneller es sich bewegt, bräuchte man auch immer mehr Energie, um es weiter zu beschleunigen. Um die Lichtgeschwindigkeit zu erreichen, wäre unendlich viel Energie nötig.
Optischer Dopplereffekt
Analog zum Dopplereffekt bei Schallwellen gibt es auch einen optischen Dopplereffekt.
$\frac{\lambda_B}{\lambda_Q} = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$
Die Wellenlänge des Lichts erscheint einem Beobachter ($\lambda_B$) demnach kürzer oder länger, je nachdem, ob er sich der Quelle ($\lambda_Q$) nähert oder von ihr entfernt. Beobachten kann man diesen Effekt in Form der Rotverschiebung der Galaxien. Viele Galaxien entfernen sich von unserer. Dabei wird die Wellenlänge gestreckt, also nach "rot verschoben". Ein Objekt, welches sich nähert, würde dagegen "blau verschoben" sein

Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Spezielle Relativitätstheorie (13 Videos, 3 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Spezielle Relativitätstheorie (13 Arbeitsblätter)
-
 Der Äther und die Physik vor Einstein
PDF anzeigen
Der Äther und die Physik vor Einstein
PDF anzeigen -
 Spezielle Relativitätstheorie – Grundprinzipien
PDF anzeigen
Spezielle Relativitätstheorie – Grundprinzipien
PDF anzeigen -
 Gleichzeitigkeit in verschiedenen Inertialsystemen
PDF anzeigen
Gleichzeitigkeit in verschiedenen Inertialsystemen
PDF anzeigen -
 Zeitdilatation
PDF anzeigen
Zeitdilatation
PDF anzeigen -
 Längenkontraktion
PDF anzeigen
Längenkontraktion
PDF anzeigen -
 Relativistische Massenzunahme – ist Masse wirklich relativ?
PDF anzeigen
Relativistische Massenzunahme – ist Masse wirklich relativ?
PDF anzeigen -
 Raumzeit und Minkowski-Diagramme
PDF anzeigen
Raumzeit und Minkowski-Diagramme
PDF anzeigen -
 Invariante Größen – Raum-Zeit und Impuls-Energie
PDF anzeigen
Invariante Größen – Raum-Zeit und Impuls-Energie
PDF anzeigen -
 Minkowski-Diagramme
PDF anzeigen
Minkowski-Diagramme
PDF anzeigen -
 Lorentztransformation – Verbindung von Zeit und Ort
PDF anzeigen
Lorentztransformation – Verbindung von Zeit und Ort
PDF anzeigen -
 Addition von Geschwindigkeiten in der speziellen Relativitätstheorie
PDF anzeigen
Addition von Geschwindigkeiten in der speziellen Relativitätstheorie
PDF anzeigen -
 Optischer Dopplereffekt
PDF anzeigen
Optischer Dopplereffekt
PDF anzeigen -
 Einsteins Postulate
PDF anzeigen
Einsteins Postulate
PDF anzeigen
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt































