Chaostheorie

Inhaltsverzeichnis zum Thema

• Womit beschäftigt sich die Chaostheorie?
• Wichtige Begriffe der Chaostheorie
• Beispiele für einfache deterministische chaotische Systeme
• Chaos und Daten

Womit beschäftigt sich die Chaostheorie?

Das Chaos selbst ist die Beschreibung eines Systems, welches sensitiv auf die Änderung der Anfangsbedingungen reagiert. Jede Aktion hat eine scheinbar unerwartbare Reaktion zur Folge. Die Chaostheorie beschäftigt sich nur mit einer bestimmten Form dieses Chaos: mit dem deterministischen Chaos. Bei diesen Systemen ist es so, dass sie klaren physikalischen Gesetzen folgen, aber eine kleine Änderung der Anfangsbedingungen große Auswirkungen auf das Ergebnis hat. Solche Systeme können sich anfänglich noch harmonisch verhalten, ab einem bestimmten Punkt zeigt sich dann jedoch eine höhere Bifurkation (Verzweigung) der beobachtbaren Zustände.

Wichtige Begriffe der Chaostheorie

Deterministische chaotische Systeme lassen sich beschreiben:

• Durch die Trajektorie. Diese ist die genaue Verlaufslinie des chaotischen Systems. Diese Bahn erhält man, wenn man zu jedem Zeitpunkt $t$ den Zustand des chaotischen Systems in allen Dimensionen beschreibt und diese in ein Phasendiagramm einträgt.
• Durch den Attraktor. Dieser ist die wiederkehrende Ähnlichkeit in der Trajektorie. Die gesamte Trajektorie ist dabei nicht periodisch, besitzt aber eine Selbstähnlichkeit.
• Durch die Bifurkation. Diese ist die Aufspaltung eines stabilen Zustandes in mehrere Zustände, von denen zumindest einer instabil ist.
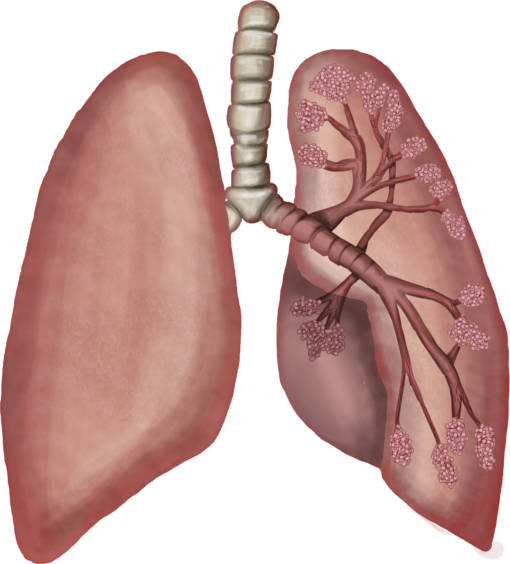
• Und durch die bildliche Entsprechung eines Fraktals. Fraktale sind häufig verzweigte und selbstähnliche geometrische Muster, die sich ins Unendliche fortsetzen. Diese entsprechen einer mathematischen Menge. Auch in der Natur finden sich fraktalähnliche Strukturen wie in deiner Lunge.

Beispiele für einfache deterministische chaotische Systeme

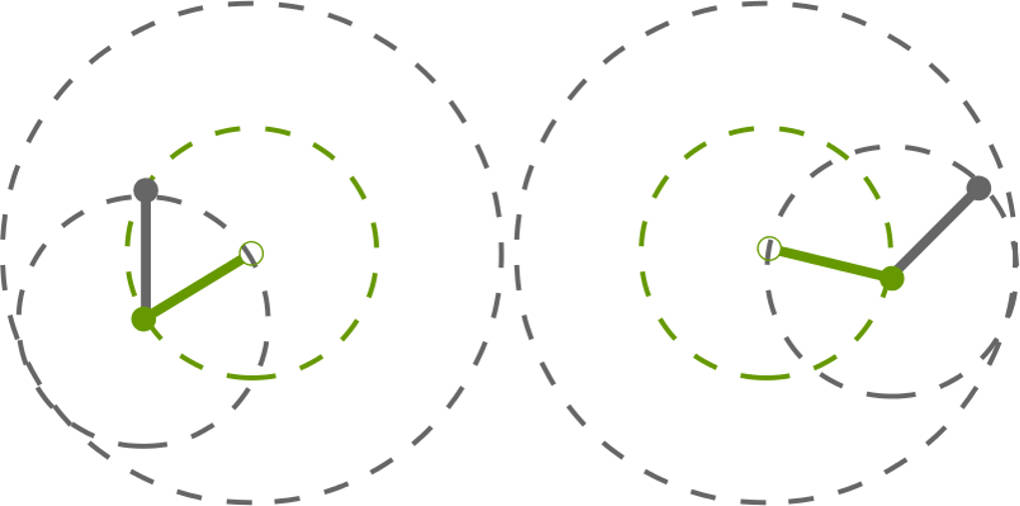
Ein mögliches Beispiel für ein deterministisches chaotisches System ist das Doppelpendel. Bei diesem Pendel wurde am Ende eines starren Pendels noch ein weiteres starres Pendel angebracht. Da die beiden Pendel meist die gleiche Länge besitzen, kann sich die Spitze des zweiten Pendels zu einem beliebigen Zeitpunkt $t$ überall auf der kreisförmigen Fläche mit einem Radius $r$ von der doppelten Pendellänge befinden. Wo genau, hängt sehr stark von den Startbedingungen ab.

Chaos und Daten

Die Vorhersage von deterministischen chaotischen Systemen wird durch umfangreiche, verlässlich gesammelte Daten vereinfacht. Würde man zum Beispiel beim Doppelpendel die Bewegungsabläufe unter sehr vielen Anfangsbedingungen kennen, würde sich der Weg des Pendels einfacher vorhersagen lassen. Umfangreiche Daten liegen bei der Wetteraufzeichnung vor. Diese erleichtern die heutige Wettervorhersage und bilden die Grundlage vieler Modelle zur Wettervorhersage.

Ein besonderer, aber auch bedenklicher Einsatz von datenbasierten Vorhersagen ist die Vorhersage von spontanem menschlichen Verhalten. Jeder der sich im Internet bewegt, hinterlässt häufig unbewusst Daten. Andere teilen sogar häufig unbedacht, aber komplett freiwillig alle Informationen über sich selbst und über Freunde in den sozialen Medien. Durch die derzeit schon gesammelten Daten zu Personen, können Programme viel besser mögliche spontane Interessen und Verhaltensweisen vorhersagen. Diese dienen dann dazu, sehr passgenaue Manipulationen, zumeist am Kaufverhalten, vorzunehmen. Aber auch die gezielte Manipulationen von persönlichen Einstellungen sind vorstellbar.