Mechanische Schwingungen

Inhaltsverzeichnis zum Thema

• Was ist eine mechanische Schwingung?
• Das Federpendel
• Kenngrößen einer Schwingung
• Das Fadenpendel
• Erzwungen Schwingung und Resonanz

Was ist eine mechanische Schwingung?

Schwingungen sind in der Physik allgegenwärtig. Sie tauchen in der Quantenmechanik, der Elektrizitätslehre, in der Mechanik und in vielen weiteren Gebieten auf. Dabei ist der mathematische Formalismus stets derselbe und wenn du ihn einmal richtig verstanden hast, kannst du ihn im Prinzip auf jedes physikalische Teilgebiet übertragen. Daher macht es Sinn, sich zunächst mit den einfachen mechanischen Schwingungen zu beschäftigen.

Eine Schwingung ist definiert als eine zeitlich periodische Bewegung eines Oszillators um seine Gleichgewichtslage. Bei mechanischen Schwingungen ist der Oszillator meist eine schwingende Masse. In der Elektrizitätslehre kennt man den elektromagnetischen Schwingkreis. Hier wäre der Oszillator der Strom im Stromkreis beziehungsweise die elektrischen und magnetischen Felder.

Lenkst du einen Oszillator aus seiner Ruhelage aus, so fügst du ihm Energie hinzu. Die rücktreibende Kraft sorgt dann dafür, dass der Oszillator zeitlich periodisch schwingt. Das bedeutet, dass der Oszillator in regelmäßigen zeitlichen Abständen immer wieder von seinem Umkehrpunkt durch seine Gleichgewichtslage zum zweiten Umkehrpunkt und wieder zurückschwingt. Dabei geht die anfangs hinzugefügte Energie gemäß der Energieerhaltung niemals verloren, aber sie wandelt sich in andere Energieformen um. Daher ist die Energieerhaltung ein guter mathematischer Ansatz um Schwingungen zu berechnen.

Trägst du eine harmonische Schwingung in ein Diagramm ein, so ergibt sich eine Sinuskurve.

Das Federpendel

Nun, da du die wichtigsten Begrifflichkeiten einer Schwingung kennengelernt hast, kannst du dich folgendem Beispiel widmen: dem Federpendel.

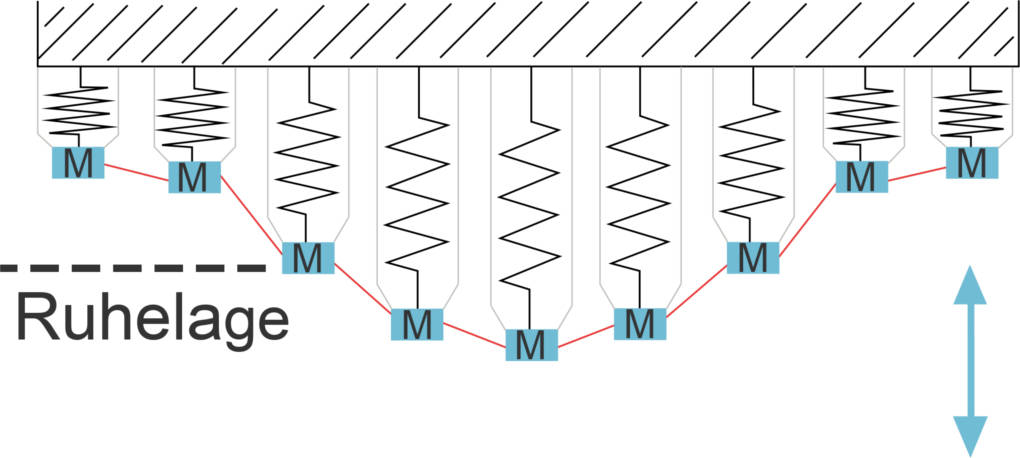
Ein Federpendel besteht aus einer Masse, die an einer Feder aufgehängt ist. Wenn du das Federpendel einfach frei hängen lässt, dann schwingt es nicht, sondern befindet sich in seiner Gleichgewichtslage. Wie du eben gelernt hast, musst du einem Oszillator zunächst Energie zufügen, damit er schwingt: Lenkst du das Federpendel nach oben aus, so fügst du ihm Spannenergie hinzu, da du die Feder zusammenstauchst.

Die Federkraft, die hier als rücktreibende Kraft die Schwingung antreibt, lässt das Pendel nach unten schwingen. Dabei wandelt sich Spannenergie in kinetische Energie um. Wenn das Pendel wieder seine Gleichgewichtslage erreicht, hat es eine gewisse Geschwindigkeit. Daher verharrt es nicht in seiner Gleichgewichtslage, sondern schwingt nach unten weiter und das Federpendel dehnt sich aus.

Wenn die Feder die Bewegung des Pendels nach unten zum Stillstand gebracht hat, befindet sich das Pendel in seinem unteren Umkehrpunkt. Die Feder beginnt nun sich wieder zusammenzuziehen (rücktreibende Kraft), was das Pendel wieder nach oben in Bewegung versetzt. Dabei durchläuft das Pendel wieder seine Gleichgewichtslage und erreicht wieder seinen Ausgangspunkt. Dabei wandelt sich kinetische Energie wieder in Spannenergie.

Kenngrößen einer Schwingung

Eine jede Schwingung, so auch die des Federpendels, lässt sich durch drei Kenngrößen beschreiben: Die Amplitude ist der Abstand zwischen der Gleichgewichtslage und dem Umkehrpunkt. Beim Federpendel ist dies gerade die Größe der anfänglichen Auslenkung. Die Schwingungsdauer $T$ gibt an, wie lange es dauert, bis sich das Pendel wieder in seiner Ausgangslage befindet. Beim Federpendel hängt die Schwingungsdauer von der Masse $m$ und der Härte der Feder $D$ hab und sie berechnet sich zu

$T=2\pi\sqrt{\frac{m}{D}}$.

Die Frequenz $f$ ist der Kehrwert der Schwingungsdauer und gibt an, wie viele Schwingungen pro Sekunde durchgeführt werden.

Das Fadenpendel

Das Fadenpendel gehört neben dem Federpendel zu den klassischen Beispielen einer mechanischen Schwingung. Bei einem Fadenpendel handelt es sich um eine Masse, die an einem Faden aufgehängt ist. Lenkst du das Fadenpendel aus, wird es durch die Schwerkraft zur Schwingung angeregt. Die rücktreibende Kraft bei einem Fadenpendel ist also die Schwerkraft.

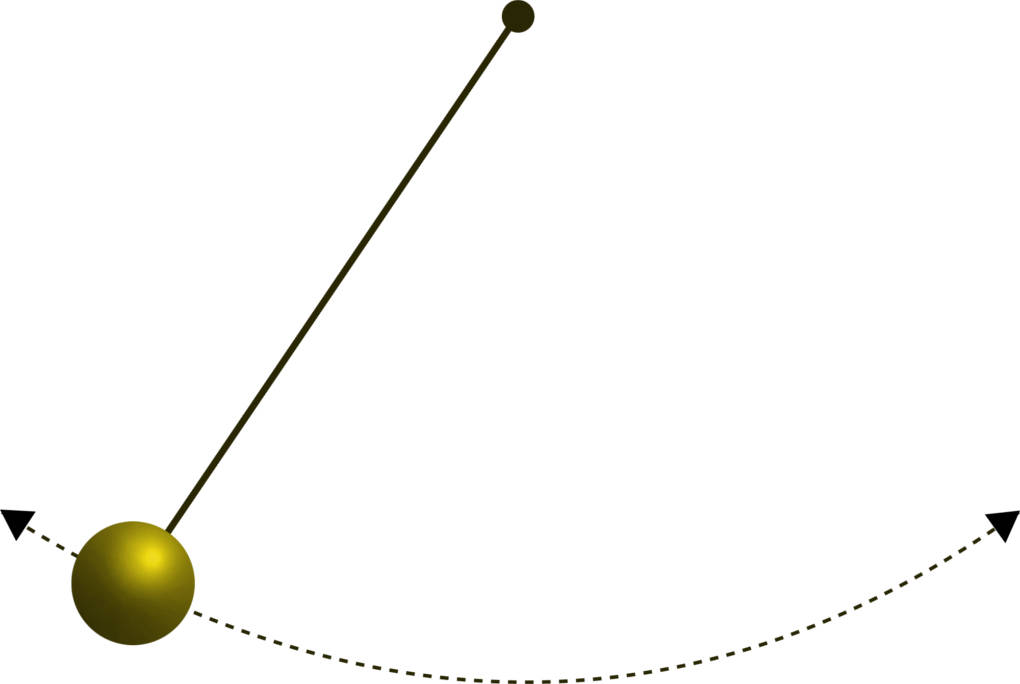
Es lässt sich herleiten, dass sich die Schwingungsdauer eines Fadenpendels aus

$T=2\pi\sqrt{\frac{l}{g}}$

berechnet. Du siehst, dass der Ortsfaktor $g$, der die Schwerkraft bestimmt, genauso eingeht wie die Federkonstante beim Federpendel. Dies ist auch logisch, da die Schwerkraft beim Federpendel dieselbe Aufgabe wie die Federkraft beim Federpendel hat, nämlich die Schwingung anregen.

Überraschend ist, dass die Schwingungsdauer eines Fadenpendels nicht von seiner Masse, sondern von seiner Länge $l$ abhängt. Ebenso ist die Auslenkung unbedeutend. Daher geht auch eine alte Pendeluhr immer gleich schnell, egal wie weit du sie auslenkst. Nun solltest du in der Lage sein, dich einmal selbst an Aufgaben zur mechanischen Schwingung zu versuchen.

Erzwungen Schwingung und Resonanz

Du hast nun das Federpendel und das Fadenpendel kennengelernt und erfahren, wie du seine Schwingungsdauer berechnen kannst. Dabei wurde bisher immer davon ausgegangen, dass das Pendel frei schwingt. Man sagt es führt eine Eigenschwingung mit seiner Eigenfrequenz aus.

Allerdings kannst du ein Fadenpendel natürlich auch in der Hand halten und die Frequenz der Schwingung vorgeben. Dann wirst du sehen, dass das Pendel nach einiger Zeit in der Frequenz schwingt, die du vorgegeben hast. Dann führt es eine erzwungene Schwingung in seiner Erregerfrequenz durch. Dabei kann es zu folgender Besonderheit kommen:

Stell dir vor, du schubst jemanden beim Schaukeln an und zwar immer im genau richtigen Moment. Die Folge ist, dass derjenige immer höher schaukelt. Physikalisch gesehen ist dies eine Resonanz. Diese tritt dann auf, wenn die Erregerfrequenz gleich der Eigenfrequenz der Schwingung ist. Die Amplitude der Schwingung wird dann immer größer, was zu einer Resonanzkatastrophe führen kann. So können etwa Gebäude bei Erdbeben oder Brücken bei starkem Wind einbrechen. Resonanz kann aber auch positiv sein, wie beim Resonanzkörper einer Gitarre.