Symmetrie

Inhaltsverzeichnis zum Thema

• Was ist Symmetrie?
• Achsensymmetrie
• Punktsymmetrie
• Drehsymmetrie

Was ist Symmetrie?

Eine Figur heißt symmetrisch, wenn sie entweder durch Spiegelung an einer Achse oder durch Drehung um einen Punkt auf sich selbst abgebildet werden kann. Hier lernst du mehr über die Merkmale der verschiedenen Symmetrieformen und wie du beispielsweise den Unterschied zwischen Achsensymmetrie und Punktsymmetrie erkennst.

Schaue dir die Ampelmännchen an. Ist eines von den beiden symmetrisch? Wenn ja, welches? Das rote Männchen ist von vorne zu sehen. Wenn du dieses Männchen durch eine Linie in der Mitte teilst, entstehen zwei genau gleich aussehende, gleichgroße Teile. Die Teile sind kongruent oder auch deckungsgleich. Das ist bei dem grünen Männchen nicht so. Das rote Ampelmännchen ist also symmetrisch und das grüne nicht.

Achsensymmetrie

Wenn du wie beim roten Ampelmännchen eine Gerade durch eine Figur legen kannst und sie die Figur in zwei deckungsgleiche Hälften teilt, nennt man das Achsensymmetrie.

Du erkennst, ob eine Figur achsensymmetrisch ist, wenn du einen Spiegel an eine Hälfte der Figur senkrecht zur Zeichenebene stellst. Wenn das Spiegelbild und die andere Hälfte gleich sind, hast du eine achsensymmetrische Figur vor dir. Die Linie, auf welcher du den Spiegel auflegst, ist die Symmetrieachse oder Spiegelachse. Hier siehst du ein Beispiel für eine achsensymmetrische Figur, einen Drachen:

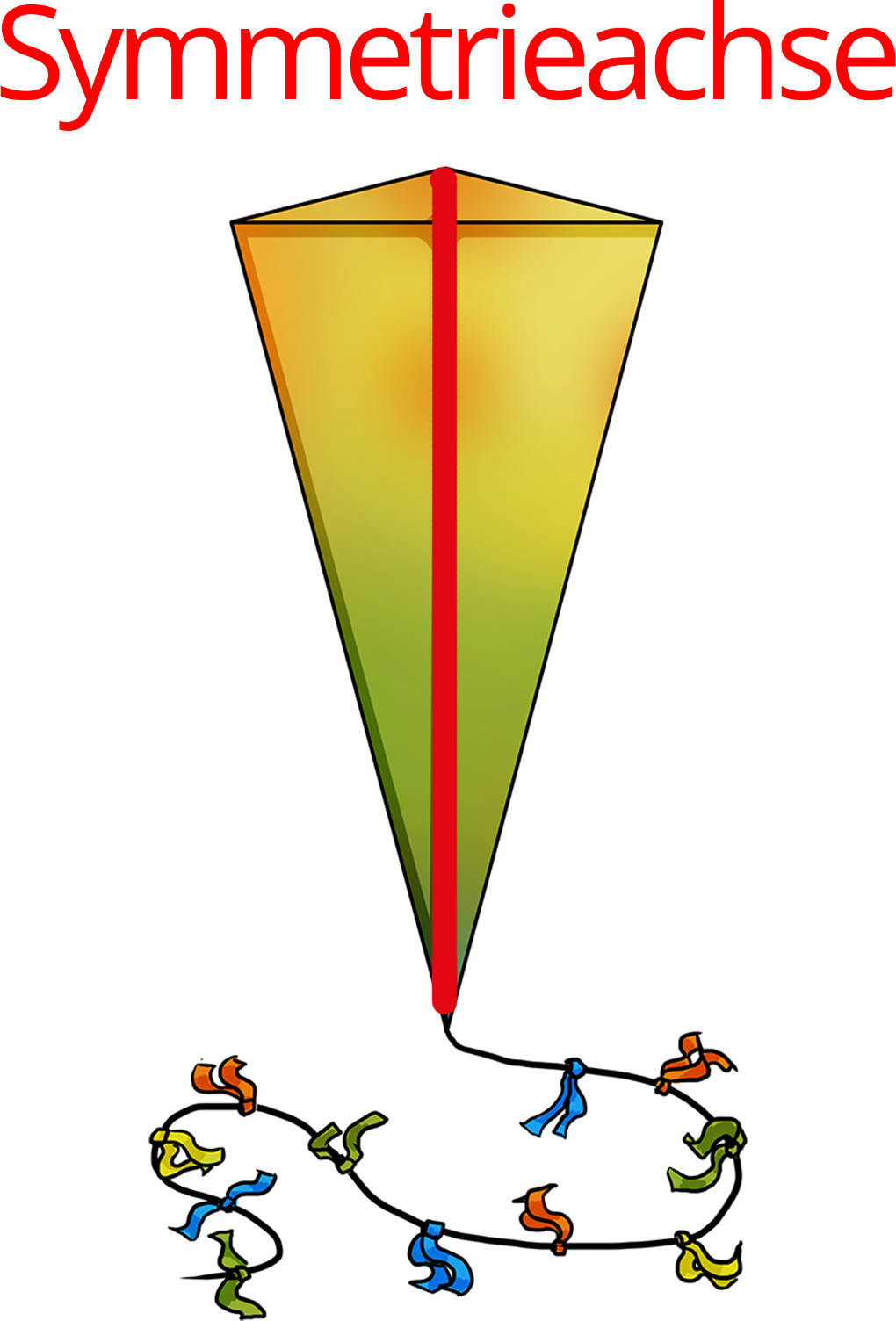
Du kannst achsensymmetrische Figuren auf verschiedene Arten erstellen:

• Du machst einen Tintenklecks auf ein Blatt Papier. Nun faltest du das Papier so, dass ein leerer Teil des Papiers auf dem Klecks aufliegt. Zuletzt faltest du das Papier wieder auf. Auf beiden Seiten der Faltlinie siehst du nun den gleichen Klecks. Du hast den Klecks gespiegelt. Die Faltlinie ist übrigens auch die Spiegelachse.
• Du kannst auch ein Blatt Papier falten und dann an der Faltlinie eine Figur ausschneiden. Wenn du nun das Papier wieder auffaltest, siehst du eine achsensymmetrische Figur.
• Übertrage eine Figur, zum Beispiel ein Dreieck, auf einem Gitterpapier Punkt für Punkt, indem du sie an einer Symmetrieachse spiegelst. Wenn du die gespiegelten Punkte miteinander verbindest, bekommst du eine Spiegelfigur der Ausgangsfigur.

Bild und Spiegelbild bei einer Achsenspiegelung sind kongruent oder auch deckungsgleich zueinander.

Punktsymmetrie

Wie kannst du erkennen, ob eine Figur punktsymmetrisch ist? Es gibt einen Punkt, um den du die Figur um 180 $^\circ$ drehen kannst. Die gedrehte Figur ist deckungsgleich mit der Ausgangsfigur. Dieser Punkt wird als Symmetriepunkt bezeichnet. In diesem Bild kannst du am Beispiel eines Dreiecks sehen, wie eine Punktspiegelung durchgeführt wird:

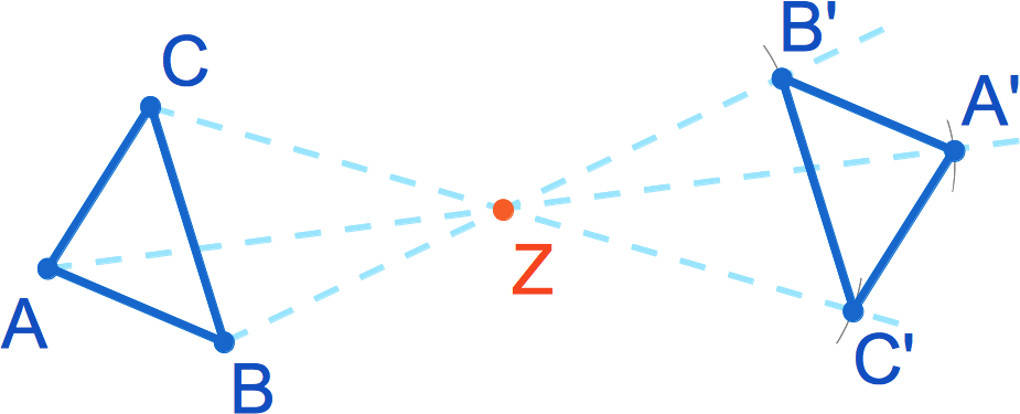
• Die Spiegelung wird an einem Punkt Z durchgeführt.
• Jeder Eckpunkt des Dreiecks wird mit Z verbunden. Dies erkennst du an den gestrichelten Linien.
• Dann wird der Abstand jedes Eckpunktes zu Z gemessen.
• Dieser Abstand wird über Z hinaus abgetragen.
• So erhältst du zu jedem Eckpunkt den Spiegelpunkt.
• Zuletzt verbindest du die Spiegelpunkte der Eckpunkte und erhältst so das gespiegelte Dreieck.

Das Ausgangsdreieck sowie das gespiegelte Dreieck sind deckungsgleich.

Drehsymmetrie

Eine Figur ist drehsymmetrisch, wenn sie nach einer Drehung um einen Winkel, der kleiner ist als 360 $^\circ$, wieder genau gleich aussieht, also deckungsgleich zur Ausgangsfigur ist. Die Punktsymmetrie ist also eine Drehsymmetrie mit dem Drehwinkel 180 $^\circ$. Hier siehst du eine drehsymmetrische Figur mit dem Drehwinkel 90 $^\circ$:

Wenn du diese Figur um 90 $^\circ$ drehst, ist die gedrehte Figur wieder gleich der Ausgangsfigur. Damit ist diese Figur auch punktsymmetrisch, da sie auch durch Drehung um 180 $^\circ$ wieder gleich der Ausgangsfigur ist.

Übrigens: Diese Figur ist auch achsensymmetrisch. Es gibt Figuren, die achsensymmetrisch und punktsymmetrisch sind. Das gilt zum Beispiel auch für ein Quadrat.