Prozentrechnung – Anwendungsaufgaben

Inhaltsverzeichnis zum Thema

• Prozentrechnung
• Rabatt-Aktion: $W$ ist gesucht.
• Bücherregal: $p$ ist gesucht.
• Schulklasse: $G$ ist gesucht.
• Merkhilfe

Prozentrechnung

Die Prozentrechnung kommt in vielen Bereichen vor:

• Eine Jeans wird um $15~\%$ reduziert.
• Auf viele Waren, die du kaufen kannst, wird eine Mehrwertsteuer in Höhe von $19~\%$ erhoben.
• $45~\%$ aller Tore, die der FC Bayern München in dieser Saison geschossen hat, fielen in der zweiten Halbzeit.
• Der Anteil der Frauen an der Gesamtbevölkerung in Deutschland beträgt $50,5~\%$ (Stand: 2018).

Mach dich mal auf die Suche, in welchen Zusammenhängen Prozent vorkommt.

All den obigen Beispielen ist gemeinsam, dass jeweils ein Anteil an etwas Ganzem betrachtet wird.

Kommen wir nun zur Bedeutung des Wortes „Prozent“. Dieses kommt aus dem Lateinischen und heißt übersetzt „für Hundert“ oder „pro Hundert“.

Es werden die folgenden Größen verwendet:

• der Grundwert $G$, also das Ganze,
• der Prozentwert $W$, der Anteil, und
• der Prozentsatz $p$.

Merke dir: Der Grund- und der Prozentwert haben stets die gleiche Einheit.

In der Prozentrechnung nutzt du die folgende Formel:

$\frac{W}{G}=\frac{p}{100}$

Je nach Aufgabenstellung kannst du diese Formel umstellen.

Übrigens: Ein Spezialfall der Prozentrechnung ist die Zinsrechnung.

Im Folgenden siehst du an verschiedenen Beispielen, wie du die Prozentrechnung anwenden kannst.

Rabatt-Aktion: $W$ ist gesucht.

Ein Bekleidungsgeschäft wirbt mit dem folgenden Rabatt zur Feier seines fünfzehnjährigen Bestehens: Auf jeden Einkauf gewähren wir $15~\%$ Rabatt.

Paul rechnet seinen Einkauf zusammen und kommt auf $72~\text{€}$. Nun überlegt er sich, wie viel er schließlich nach Abzug des Rabatts bezahlen muss. Er legt los: Zuerst überlegt er sich, welche Größen er kennt und welche gesucht ist.

• Der Grundwert $G=72$ ist bekannt. Der Einfachheit halber lässt er in der folgenden Rechnung die Einheit $\text{€}$ weg.
• Auch den Prozentsatz kennt er: $p=15~[\%]$.
• Er möchte nun den Prozentwert ausrechnen. Dieser entspricht schließlich dem gewährten Rabatt.

Los geht's: Paul setzt die Größen in die obige Formel ein und formt diese um:

$\begin{array}{rclll} \frac{W}{72}&=&\frac{15}{100}&|&\cdot 72\\ W&=&\frac{15}{100}\cdot 72\\ W&=&10,8 \end{array}$

Nun hat Paul den Rabatt von $10,80~\text{€}$ herausgefunden. Diesen muss er noch von dem Grundwert abziehen: $72~\text{€}-10,80~\text{€}=61,20~\text{€}$.

Für seinen Einkauf muss Paul nach Abzug des Rabatts $61,20~\text{€}$ bezahlen.

Bücherregal: $p$ ist gesucht.

Paul zählt seine Bücher. Er besitzt insgesamt $150$ Bücher. Davon sind $45$ Mathe-Bücher. Mathe ist sein Lieblingsfach in der Schule. Wie hoch ist der Prozentsatz?

Dieses Mal kennt Paul den Grundwert $G=150$ und den Prozentwert $W=45$. Diese Größen setzt er in die Formel zur Prozentrechnung ein und formt diese um:

$\begin{array}{rclll} \frac{45}{150}&=&\frac{p}{100}&|&\cdot 100\\ p&=&\frac{45}{150}\cdot 100\\ p&=&30 \end{array}$

$30~\%$ von Pauls Büchern sind Mathe-Bücher. Wie viele sind das denn bei Dir?

Das hätten wir auch mit dem Dreisatz lösen können: Der Grundwert entspricht $100\%$. Wie viel Prozent entspricht dann dem Prozentwert?

• Zuerst dividierst du $G=150$ durch $150$, um auf $1$ zu kommen.
• Dann multiplizierst du mit $45$, um auf $W=45$ zu kommen. So kommst du zu den diesem Prozentwert entsprechenden $30\%$.

Warum kannst du das so machen? Die Prozentrechnung ist ein Beispiel für eine direkt proportionale Zuordnung. Dabei bedeutet direkt proportional: Je mehr desto mehr.

Schulklasse: $G$ ist gesucht.

In einer Schulklasse kommen $9$ Schüler mit dem Bus. Das sind $30~\%$ der gesamten Klasse. Wie viele Schüler befinden sich in der Klasse?

Weißt du schon, welche Größen du in dieser Aufgabe kennst? Richtig: $W=9$ und $p=30~[\%]$. Du möchtest $G$ berechnen. Setze die Größen in die obige Formel ein und forme nochmal um:

$\begin{array}{rclll} \frac{9}{G}&=&\frac{30}{100}&|&\text{multipliziere über Kreuz}\\ 9\cdot 100&=&30\cdot G&|&:30\\ 30&=&G \end{array}$

In der Schulklasse befinden sich also insgesamt $30$ Schüler.

Merkhilfe

Du kannst dir dieses Dreieck einprägen, um dir die jeweilige Formel zur Berechnung einer fehlenden Größe bei einer Aufgabe zur Prozentrechnung herzuleiten:

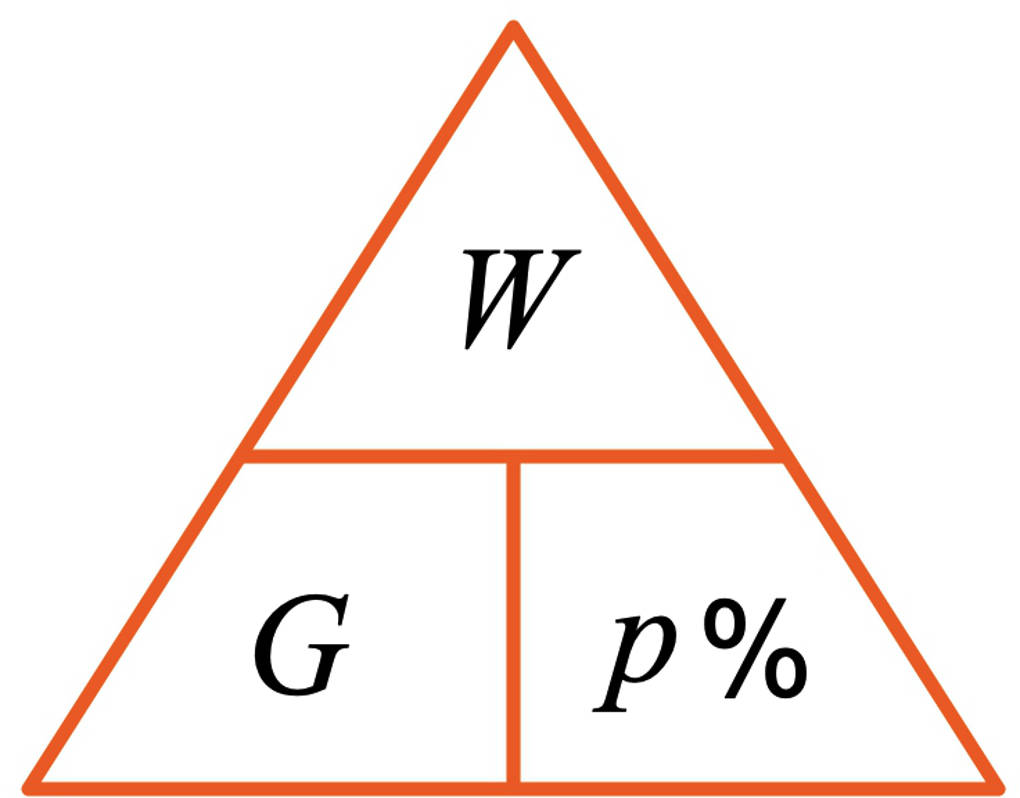
• Zur Berechnung von $W$ hältst du $W$ zu: $G$ und $p~\%$ stehen auf der gleichen Höhe. Hier multiplizierst du: $W=G\cdot p~\%$.

Bei den beiden anderen Größen ist das ein wenig anders:

• Willst du $G$ berechnen, hältst du auch hier die entsprechende Größe zu. $W$ steht über $p~\%$. Du dividierst und erhältst somit $G=\frac{W}{p~\%}$.
• Ebenso ist dies bei der Berechnung von $p~\%$. Halte auch diese Größe zu. $W$ steht über $G$. Wieder dividierst du $p~\%=\frac{W}{G}$.