Vierecke und Vielecke konstruieren
Vielleicht hast du ja mal Lust ein Quadrat zu konstruieren oder ein regelmäßiges Fünfeck. Wie das geht, lernst du hier.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Vieleck?
- Regelmäßige und unregelmäßige Vielecke
- Vierecke konstruieren
- Regelmäßige Vielecke konstruieren
Was ist ein Vieleck?
Ein Vieleck, oder auch Polygon, ist eine ebene Figur. Es hat drei oder mehr Ecken, welche nicht auf einer Geraden liegen. Von jeder Ecke gehen zwei Kanten, oder auch Seiten, zu den beiden benachbarten Ecken ab. An jeder Ecke treffen also zwei Kanten aufeinander.
Du kennst sicher schon einige Vielecke, z.B.
- das Dreieck,
- das Viereck, oder auch Tetragon,
- das Fünfeck, dieses wird auch Pentagon genannt, oder
- das Sechseck, welches auch Hexagon genannt wird.
Alle Vielecke haben die Eigenschaft, dass die Winkelsumme, also die Summe der Innenwinkel, gegeben ist durch $(n-2)\cdot 180^\circ$, wobei $n$ die Anzahl der Ecken ist. So beträgt die Winkelsumme
- bei Dreiecken $(3-2)\cdot 180^\circ=180^\circ$, (weil ein Dreieck $3$ Ecken hat)
- bei Vierecken $(4-2)\cdot 180^\circ=360^\circ$, (weil ein Viereck $4$ Ecken hat)
- bei Fünfecken $(5-2)\cdot 180^\circ=540^\circ$, (weil ein Fünfeck $5$ Ecken hat)
- ...
Regelmäßige und unregelmäßige Vielecke
Es gibt regelmäßige und unregelmäßige Vielecke. Bei einem regelmäßigen Vieleck sind alle Seiten gleich lang und alle Innenwinkel gleich groß.
Regelmäßige Dreiecke und Sechsecke
In dem Bild siehst du ein rotes regelmäßiges Sechseck und ein grünes regelmäßiges Dreieck. Ein regelmäßiges Dreieck wird auch als gleichseitiges Dreieck bezeichnet.
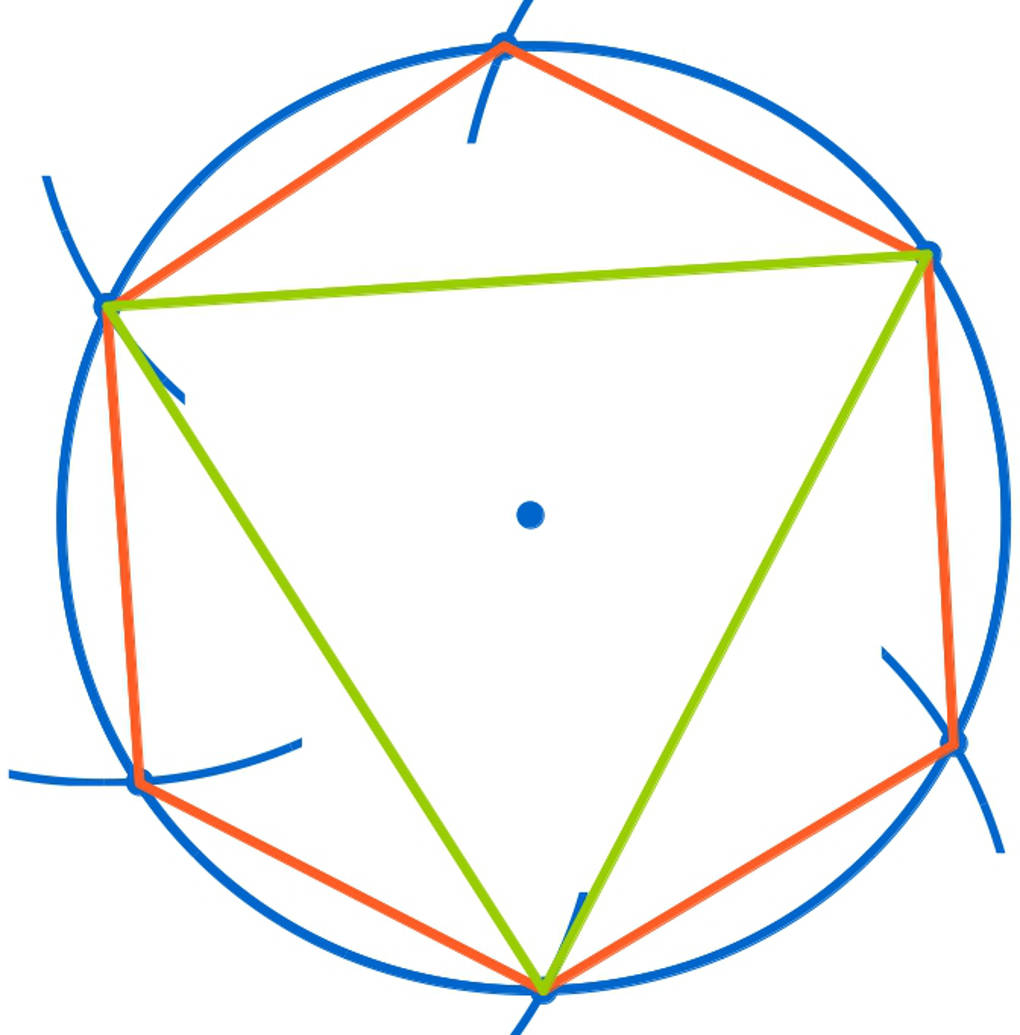
Hier siehst du, wie du ein regelmäßiges Sechseck konstruieren kannst:
- Du zeichnest einen Kreis mit dem Radius $r$.
- Dann markierst du irgendeinen Punkt auf dem Kreisrand.
- Nun trägst du in diesem Punkt einen Kreis, ebenfalls mit dem Radius $r$, ab. Der Schnittpunkt dieses Kreises mit dem Ausgangskreis ist der nächste Punkt.
- Du stichst mit dem Zirkel in diesen neuen Punkt ein und trägst wieder einen Kreis mit dem Radius $r$ ab.
- So fährst du fort, bis du sechs Punkte auf dem Kreisrand gefunden hast.
- Zuletzt verbindest du diese Punkte miteinander.
- Fertig ist das regelmäßige Sechseck.
Wenn du immer nur jeden zweiten Punkt nimmst und diese drei Punkte miteinander verbindest, erhältst du ein gleichseitiges Dreieck.
Regelmäßige Fünfecke
Auch bei der Konstruktion eines regelmäßigen Fünfecks beginnst du mit einem Kreis. Du markierst zu Beginn wieder einen Punkt irgendwo auf dem Kreisrand. Nun verbindest du diesen Punkt mit dem Mittelpunkt deines Kreises. Mit anderen Worten, du zeichnest den Radius ein. Nun trägst du einen Winkel von $72^\circ$ an der Radiuslinie ab. Dort, wo die entstandene Linie wiederum die Kreislinie schneidet, hast du einen weiteren Eckpunkt deines Fünfecks gefunden. Im nächsten Schritt trägst du wieder einen Winkel von $72^\circ$ ab. So fährst du fort, bis du alle fünf Randpunkte gefunden hast. Diese verbindest du miteinander und fertig ist das regelmäßige Fünfeck.
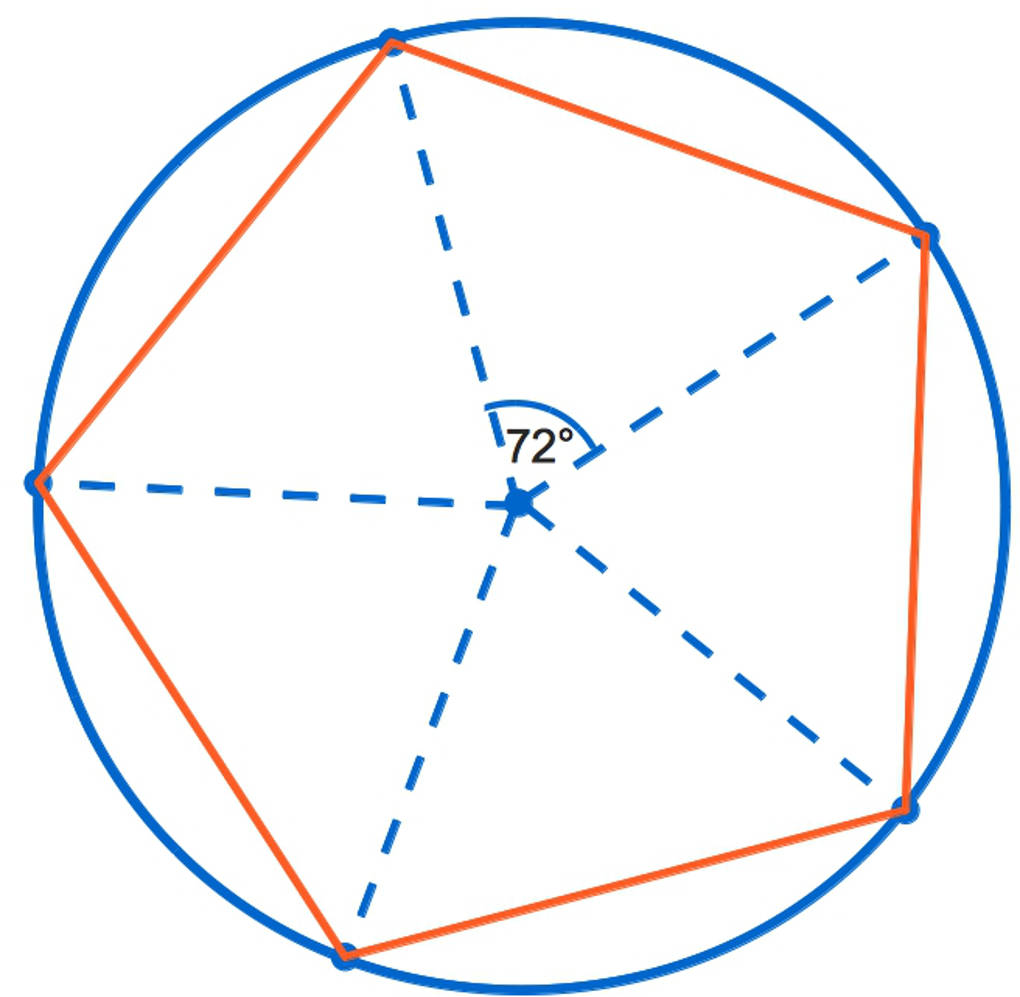
Wo kommt eigentlich der Winkel $72^\circ$ her? Der Vollwinkel beträgt $360^\circ$. Wenn du diesen durch $5$, die Anzahl der Ecken, dividierst, erhältst du $360^\circ:5=72^\circ$.
Übrigens: Auf diese Weise hättest du auch das regelmäßige Dreieck und Sechseck konstruieren können. So kannst du jedes beliebige regelmäßige Vieleck konstruieren: Dividiere den Vollwinkel durch die Anzahl der Ecken.
Vielleicht fragst du dich schon, wie das mit dem gleichseitigen Viereck ist. Dieses schauen wir uns im Folgenden gemeinsam mit den übrigen Vierecken an. Um diese besser zu verstehen, kannst du dir das Haus der Vierecke ansehen.
Vierecke konstruieren
Du möchtest Vierecke konstruieren, zum Beispiel ein Quadrat oder ein Rechteck. Im Folgenden siehst du, wie du bei der Konstruktion eines Quadrates vorgehst.
- Zeichne eine Seite des Quadrates.
- Errichte in beiden Eckpunkten dieser Seite ein Lot.
- Zeichne nun um jeden der beiden Eckpunkte einen Kreis. Der Radius ist jeweils die Seitenlänge des Quadrates.
- Jeder der beiden Kreise schneidet das Lot, welches in dem Mittelpunkt dieses Kreises errichtet wurde.
- Wenn du die so erhaltenen beiden Schnittpunkte sowohl mit den benachbarten Eckpunkten der Ausgangsseite als auch miteinander verbindest, hast du ein Quadrat konstruiert.
Ebenso kannst du ein Rechteck konstruieren.
Möchtest du ein Parallelogramm konstruieren, folgst du diesen Schritten:
- Zeichne eine Seite des Parallelogramms.
- Trage in beiden Eckpunkten den gleichen Winkel an diese Seite so an, dass die daraus resultierenden Halbgeraden parallel zueinander sind.
- Konstruiere nun eine Parallele zu der Ausgangsseite so, dass diese die beiden Halbgeraden schneidet. Diese Schnittpunkte sind die beiden fehlenden Eckpunkte des Parallelogramms.
Regelmäßige Vielecke konstruieren
Vielecke sind ebene Figuren mit $3$ oder mehr Ecken. Diese dürfen nicht auf einer Geraden liegen. Von jeder dieser Ecken gehen zwei Kanten, oder auch Seiten, zu den beiden benachbarten Ecken ab. Bei einem regelmäßigen Vieleck sind alle Seiten gleich lang und alle Innenwinkel gleich groß. Das hast du ja bereits bei einem gleichseitigen, also regelmäßigen Dreieck gesehen.
Hier siehst du, wie du ein regelmäßiges Fünfeck konstruieren kannst:
- Du beginnst mit einem Kreis.
- Markiere einen Punkt auf dem Kreisrand und verbinde diesen mit dem Mittelpunkt des Kreises. Du zeichnest also den Radius ein.
- Trage an der Radiuslinie im Mittelpunkt einen Winkel von $72^{\circ}$ an. Der freie Schenkel schneidet die Kreislinie in einem weiteren Eckpunkt des Fünfecks.
- Trage nun an diesem Schenkel im Mittelpunkt wieder den Winkel $72^{\circ}$ an.
- Fahre so fort, bis du alle $5$ Eckpunkte gefunden hast.
- Zuletzt verbindest du diese Eckpunkte zu einem regelmäßigen Fünfeck.
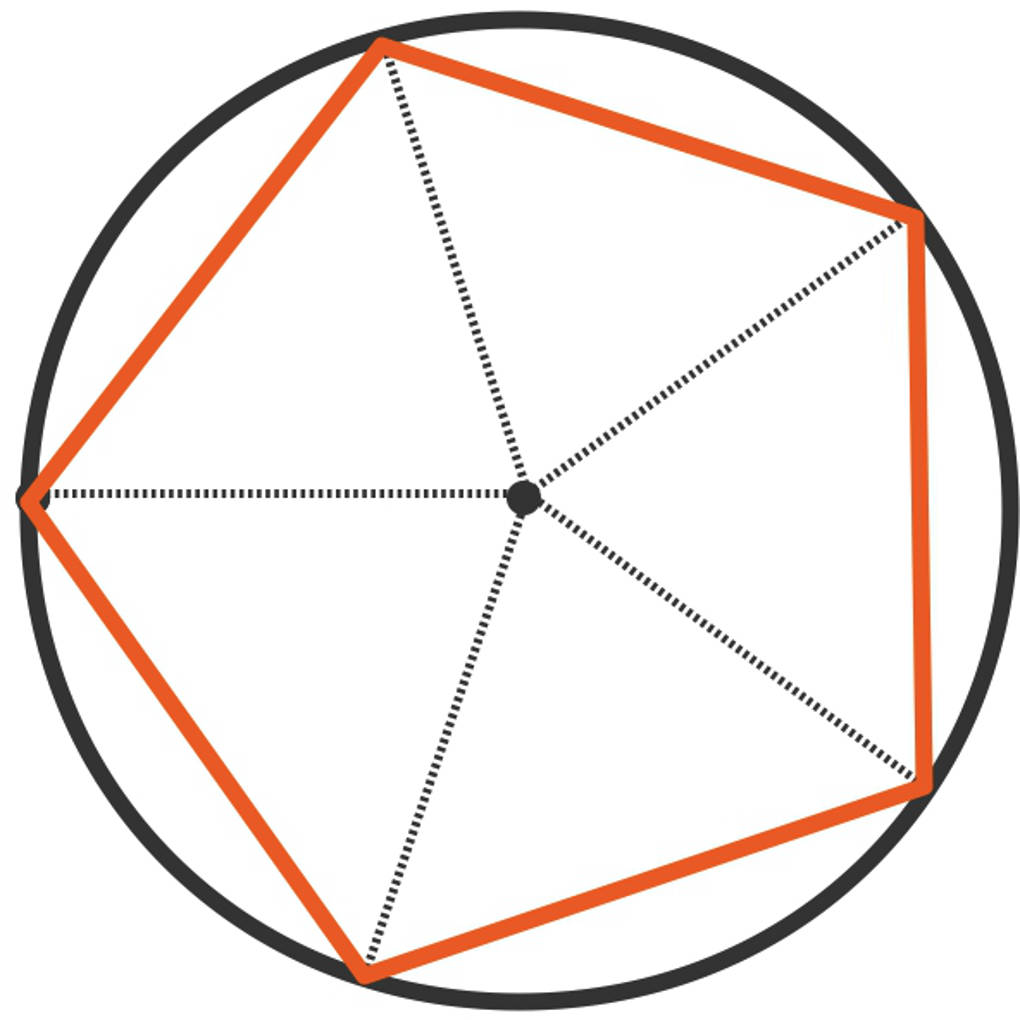
Woher kommt eigentlich der Winkel $72^{\circ}$? Diesen erhältst du, wenn du den Vollwinkel $360^{\circ}$ durch $5$, die Anzahl der Ecken, dividierst.
So kannst du übrigens jedes beliebige regelmäßige Vieleck, zum Beispiel ein in einen Kreis einbeschriebenes Achteck, konstruieren.
Alle Videos zum Thema
Videos zum Thema
Vierecke und Vielecke konstruieren (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Vierecke und Vielecke konstruieren (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen









 Eigenschaften von Vielecken
Eigenschaften von Vielecken
 Quadrate und Rechtecke konstruieren
Quadrate und Rechtecke konstruieren
 Parallelogramme zeichnen
Parallelogramme zeichnen
 Konstruktion eines Trapezes
Konstruktion eines Trapezes
 Regelmäßige Vielecke konstruieren
Regelmäßige Vielecke konstruieren









