Einheiten umrechnen – Zusammenfassung

Inhaltsverzeichnis zum Thema

• Was sind Einheiten und was sind Größen?
• Zeiteinheiten
• Längeneinheiten
• Gewichtseinheiten
• Flächeneinheiten
• Volumeneinheiten

Was sind Einheiten und was sind Größen?

Wenn du morgens zur Schule fährst, legst du eine Strecke zurück. Für diese Strecke benötigst du eine gewisse Zeit.

• Strecken werden z.B. in Meter oder Kilometer angegeben.

• Zeit wird z.B. in Minuten oder Stunden angegeben.

• Der Weg kann mit Zahlen beschrieben werden, zum Beispiel mit $1,5~km$. Daher nennt man den Weg eine Größe. Die Zahl $1,5$ ist die Maßzahl und $km$ die Maßeinheit.

• Die benötigte Zeit für diesen Weg beträgt $15~min$. Zeit ist ebenfalls eine Größe. $15$ ist die Maßzahl und $min$ die Maßeinheit.

Zeiteinheiten

Zeiteinheiten dienen dazu, Zeitspannen anzugeben. Welche Zeiteinheiten kennst du? Es gibt Sekunden ($s$), Minuten ($min$), Stunden ($h$), Tage ($d$), Wochen, Monate und Jahre.

• Wenn du an einem $100~m$-Lauf in der Schule teilnimmst, wird die Zeit in Sekunden, sogar in Hundertstel- oder Zehntel-Sekunden, gemessen.
• Eine Schulstunde dauert $45~min$. Das entspricht $45\cdot 60~s= 2700~s$, da eine Minute das Gleiche ist wie $60$ Sekunden. Eine Schulstunde wird aber normalerweise in Minuten und nicht in Sekunden angegeben.
• Wenn du morgens um 7:50 Uhr von zu Hause startest und um 13:50 Uhr wieder zurückkommst, warst du $6$ Stunden unterwegs. Du könntest auch sagen, du warst $6\cdot 60~min=360~min$ unterwegs oder $360\cdot 60~s=21600~s$.
• Bis zu deinem nächsten Geburtstag zählst du schon die Monate oder Wochen, vielleicht auch die Tage, aber doch sicher nicht die Stunden oder Minuten oder Sekunden.
• Dein Alter gibst du in Jahren an.

Hier siehst du Umrechnung für Sekunden, Minuten, Stunden und Tage:

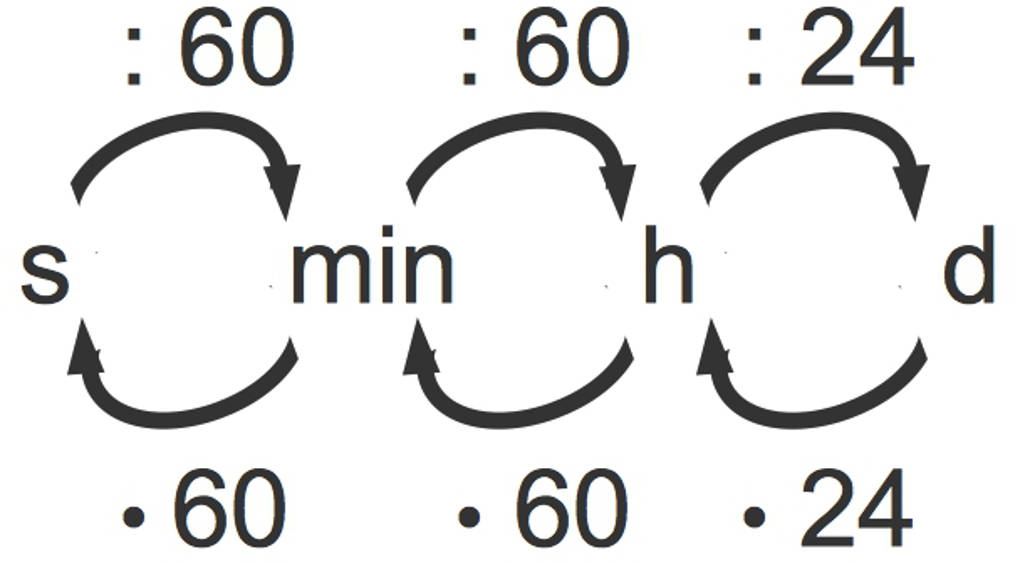
Wenn du zum Beispiel $2$ Tage in Minuten umrechnen willst, multiplizierst du zuerst mit $24$ und erhältst $48~h$. Dann multiplizierst du mit $60$ und kommst auf $2880~min$. So viele Minuten haben zwei Tage.

• Wenn du von einer kleineren in eine größere Einheit umrechnest, musst du dividieren.
• Wenn du von einer größeren in eine kleinere Einheit umrechnest, musst du multiplizieren.

Außerdem kannst du auch diese Zusammenhänge beim Umrechnen größerer Zeiteinheiten nutzen:

• Sieben Tage sind eine Woche.
• Zwölf Monate oder 365 Tage sind ein Jahr.

Längeneinheiten

Mit Längeneinheiten werden Längen gemessen. Zum Beispiel die Länge deines Schulweges oder die Strecke von Berlin nach Hamburg. Auch deine Körpergröße, die Größe deines Hundes oder die Größe einer Ameise sind Längen.

• In Millimeter ($mm$) misst du kleine Größen, zum Beispiel die Dicke deines Daumennagels.
• Zentimeter ($cm$) werden schon bei etwas größeren Größen verwendet: Deine kleine Schwester ist $87~cm$ groß oder dein Hund ist $40~cm$ groß.
• Ein Dezimeter ($dm$) ist das gleiche wie $10~cm$. Vielleicht hast du ja schon irgendwo einmal diese Maßeinheit gesehen.
• In Meter ($m$) wird die Höhe deines Hauses gemessen oder die Größe deines Vaters. Miss doch einmal die Höhe deines Zimmers. Es könnte zum Beispiel $3~m$ hoch sein.
• Für größere Längen wird die Maßeinheit Kilometer ($km$) verwendet: Die Entfernung von Berlin nach Hamburg beträgt zum Beispiel ungefähr $290~km$.

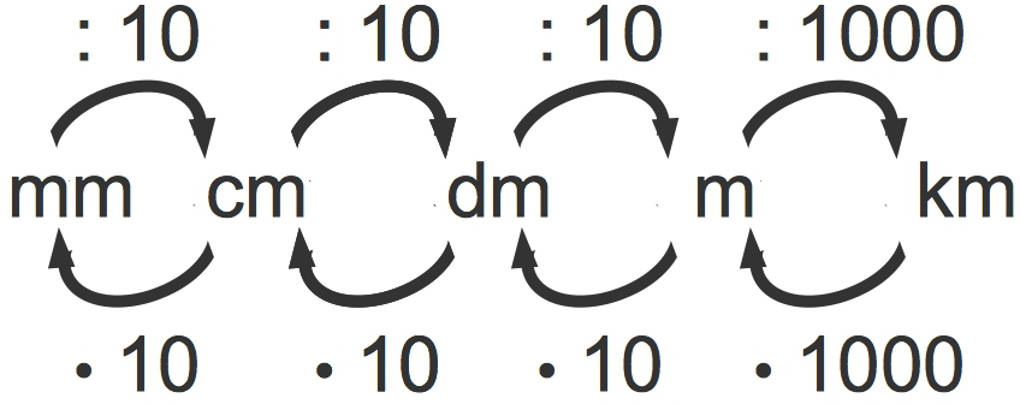
Hier siehst du die Umrechnungen der Längeneinheiten:

Gewichtseinheiten

Wenn du das Gewicht von etwas angeben willst, verwendest du Gewichtseinheiten: Milligramm ($mg$), Gramm ($g$), Kilogramm ($kg$) oder Tonne ($to$). Es gibt auch noch die Einheit Pfund für $500~g$, diese wird allerdings nicht mehr so häufig verwendet.

• Sehr kleine Gewichte werden in Milligramm angegeben.
• In Gramm gibst du zum Beispiel die Zutaten für einen Kuchen an. Schau doch einmal in ein Kochbuch und suche deinen Lieblingskuchen heraus. Mehl, Zucker und Butter werden hier häufig in Gramm angegeben.
• In Kilogramm wird dein Körpergewicht angegeben oder das Gewicht von deinem Fahrrad. Dieses könnte $11~kg$ wiegen.
• Tonnen sind eine Maßeinheit für wirklich schwere Dinge oder Lebewesen: Ein Elefant kann sieben oder acht Tonnen wiegen. Ein Auto wiegt mehr als eine Tonne. Du kannst natürlich das Gewicht eines Elefanten auch in Gramm angeben, aber diese große Zahl ist sehr unübersichtlich.

Wenn du die verschiedenen Einheiten umrechnen willst, kannst du diese Umrechnungen verwenden:

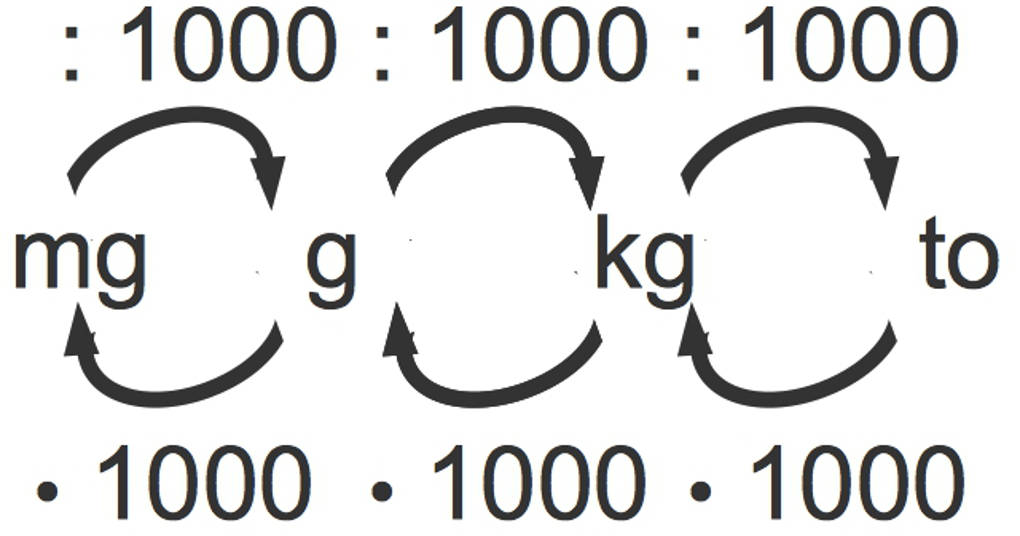
Flächeneinheiten

Flächen, wie zum Beispiel Rechtecke oder Quadrate oder Dreiecke haben einen Flächeninhalt. Dieser wird in Flächeneinheiten angegeben. Die Flächeneinheiten sehen so ähnlich aus, wie die Längeneinheiten, da steht noch eine kleine $2$. Du sagst dann Quadrat....

• Quadratmillimeter ($mm^2$): Ein flacher Stecknadelkopf hat einen Flächeninhalt von $1~mm^2$.
• Quadratzentimeter ($cm^2$): Dein Daumennagel hat einen Flächeninhalt von $1~cm^2$.
• Quadratmeter ($m^2$): Wenn du einen Teppich hast, der einen Meter lang und einen Meter breit ist, dann hat dieser Teppich den Flächeninhalt $1~m^2$. Eure Wohnung wird in Quadratmeter angegeben, zum Beispiel $96~m^2$.
• Quadratkilometer ($km^2$): Berlin hat ungefähr eine Fläche von $892~km^2$.

Es gibt noch weitere Flächeneinheiten:

• Ein Ar ($a$) ist das Gleiche wie $100~m^2$.
• Ein Hektar ($ha$) ist das Gleiche wie $10000~m^2$.

Die Umrechnungen siehst du hier.

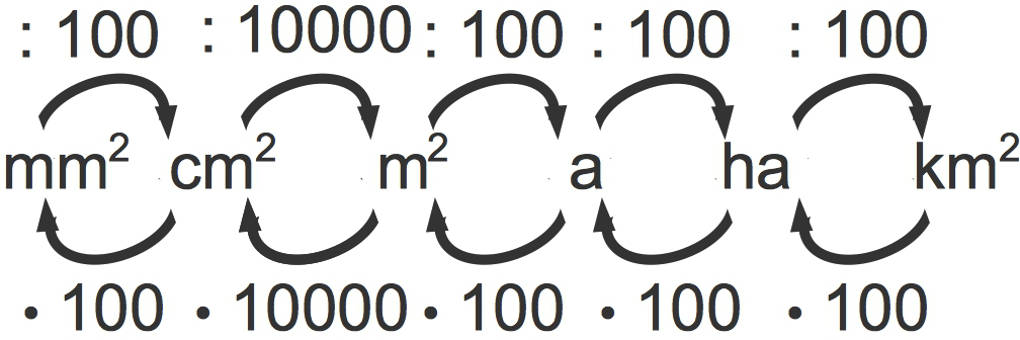
Volumeneinheiten

Volumeneinheiten verwendest du zur Berechnung des Volumens von Körpern. Auch diese sind ähnlich zu den Längeneinheiten. Dieses Mal steht eine kleine $3$ da. Du liest die Einheiten dann Kubik...:

• Kubikmillimeter ($mm^3$)
• Kubikzentimeter ($cm^3$)
• Kubikdezimeter ($dm^3$)
• Kubikmeter ($m^3$)

Du kennst Volumenangaben vielleicht auch in Liter oder Milliliter. Dies sind Hohlmaße. Wichtig ist dabei, dass du dir merkst: $10~cm\cdot 10~cm\cdot 10~cm=1~dm\cdot1~dm\cdot 1~dm=1~dm^3$ und dies entspricht einem Liter.