Flächeninhalt und Umfang von Drachenvierecken und Rauten
Es ist Herbst und du möchtest dir einen Drachen bauen. In dem Zusammenhang ist es wichtig, dass du weißt, wieviel Material du benötigst. Du musst also den Umfang und den Flächeninhalt des Drachens berechnen.
Inhaltsverzeichnis zum Thema
- Anwendung Flächeninhalt und Umfang eines Drachenvierecks
- Die Raute: Eigenschaften, Umfang und Flächeninhalt
- Das Drachenviereck: Eigenschaften, Umfang und Flächeninhalt
- Anwendungsbeispiel Flächeninhalt Drachenviereck
Anwendung Flächeninhalt und Umfang eines Drachenvierecks
Es ist Herbst und du möchtest dir einen Drachen bauen. Im Wald findest du zwei Stöcke. Du möchtest wissen, wie viel Material du zum Basteln benötigst. Du willst also den Umfang und den Flächeninhalt des Vierecks berechnen. Um dies berechen zu können, musst du wissen, ob du den Flächeninhalt eins Drachenviereck oder einer Raute bestimmen musst.

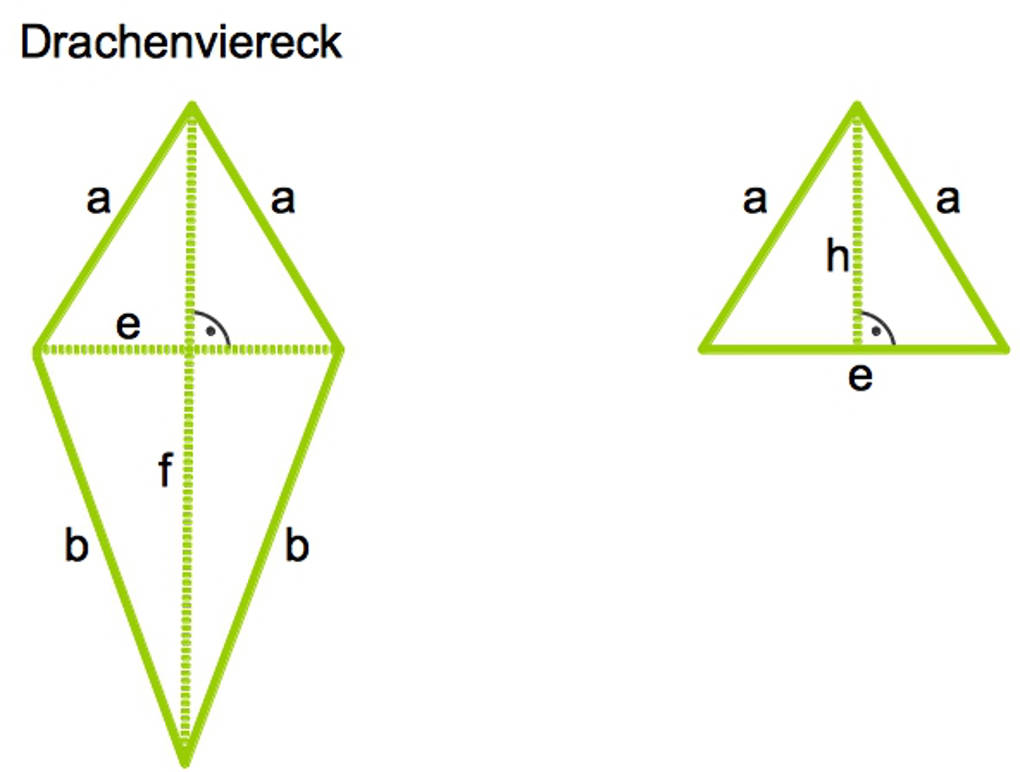
Die Raute und das Drachenviereck sind ebene Figuren mit vier Ecken, also Vierecke. Sie haben vier Seiten und vier Innenwinkel. Die Summe der Innenwinkel beträgt wie bei allen Vierecken $360^\circ$.
Im Haus der Vierecke findest du verschiedenen Vierecksarten nach ihren Eigenschaften sortiert.
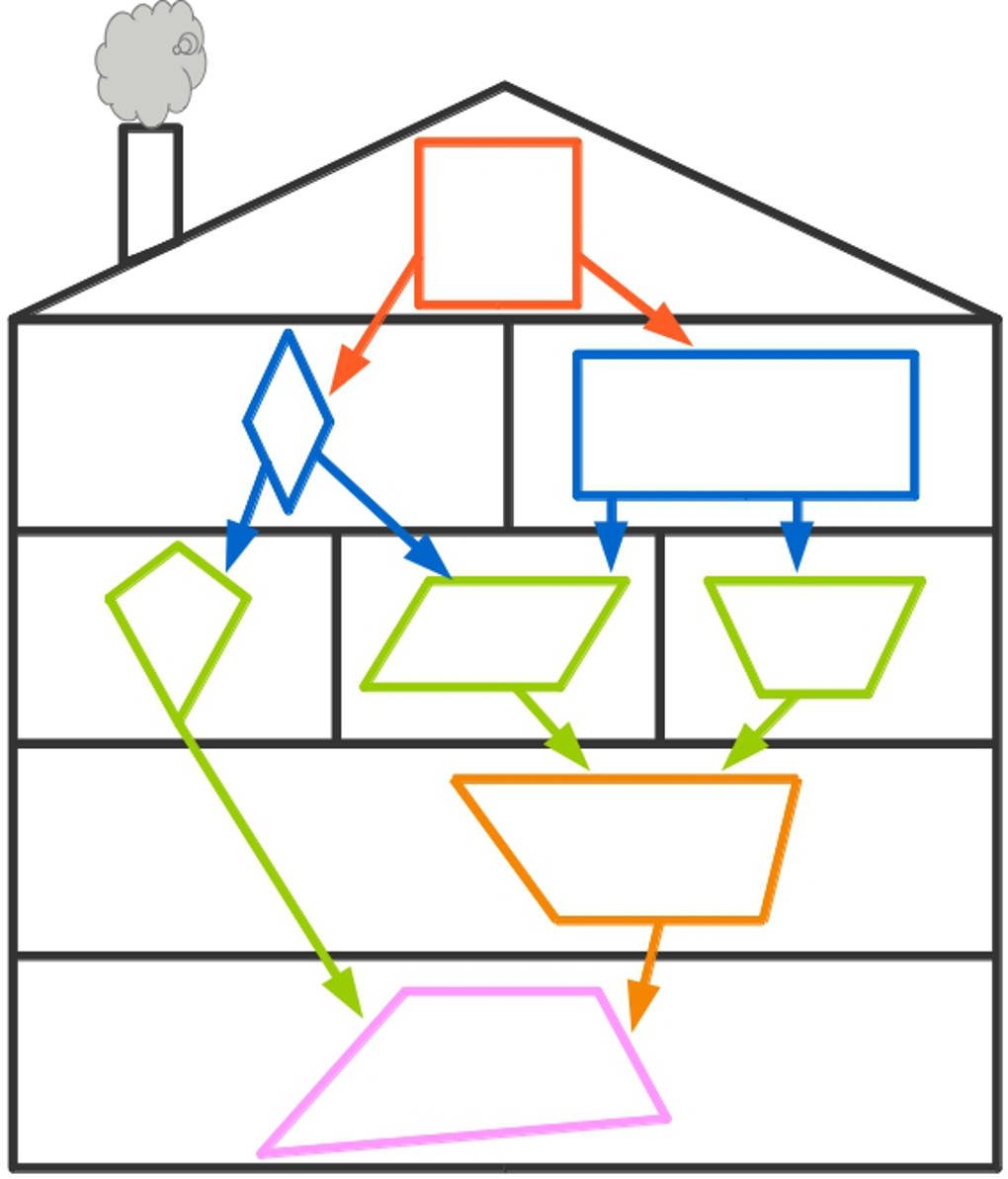
Die Raute: Eigenschaften, Umfang und Flächeninhalt
Die Raute (auch Rhombus genannt), kannst du direkt links unter dem Quadrat erkennen.
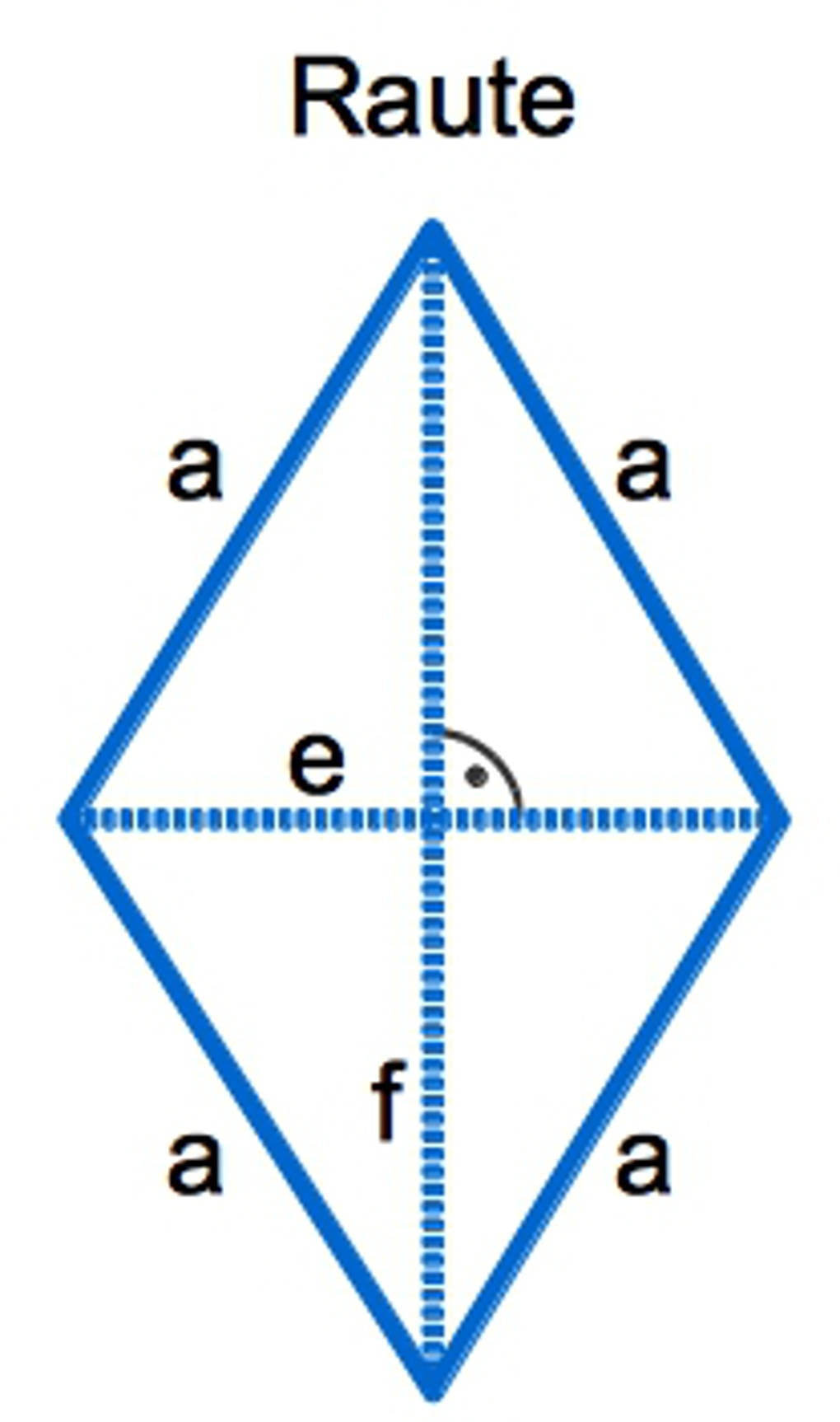
Eigenschaften Raute
- In einer Raute und einem Quadrat sind alle Seiten gleich lang.
- In einer Raute sind nicht, wie in einem Quadrat, alle Winkel gleich groß.
- Die gegenüberliegenden Winkel bei einer Raute sind gleich groß. Die benachbarten Winkel ergänzen einander auf $180^\circ$.
- Die Diagonalen $e$ und $f$ in einer Raute schneiden sich genau in der Mitte der Raute in einem rechten Winkel ($90^\circ$). Die Diagonalen halbieren damit einander.
- Jeder Innenwinkel wird durch eine Diagonale halbiert.
- Eine Raute hat zwei Symmetrieachsen auf denen die beiden Diagonalen liegen.
- Die einander gegenüberliegenden Seiten sind parallel zueinander. Die Raute ist also auch ein Parallelogramm.
Der Umfang einer Raute
Zur Berechnung des Umfang und des Flächeninhalts einer Raute werden die Eigenschaften von Vierecken genutzt.
Für den Umfang einer Raute addierst du wie bei jedem Viereck die Längen aller vier Seiten. Bei einer Raute sind alle Seiten gleich lang mit Seitenlänge $a$. Es gilt für den Umfang einer Raute folgende Formel :
$u=a+a+a+a=4a$.
Dieselbe Formel gilt auch für den Umfang eines Quadrats.
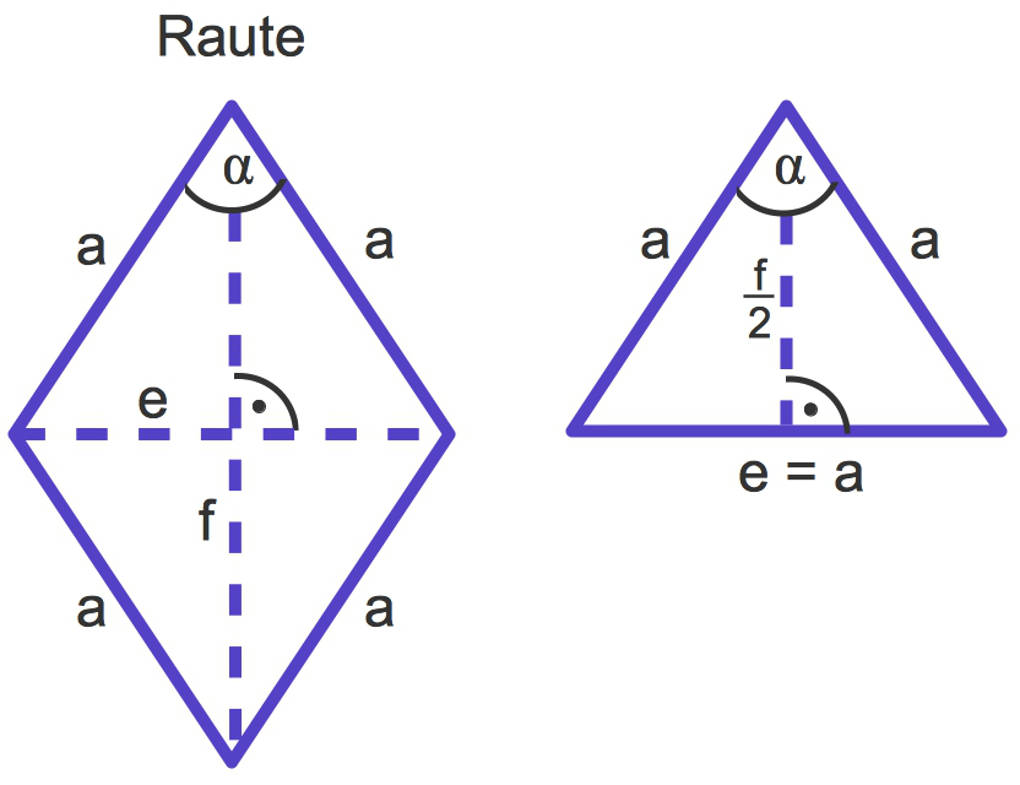
Der Flächeninhalt einer Raute
Der Flächeninhalt einer Raute kann über zwei Formeln bestimmt werden. Die erste Gleichung entspricht der Flächeninhaltsformel des Parallelograms mit der Seitenlänge $a$ und der zugehörigen Höhe $h_ {a}$.
$A=a \cdot h_ {a}=\frac{e\cdot f}2$
Die zweite Gleichung ergibt sich aus der Überlegung, dass eine Raute sich in zwei gleiche, kongruente gleichschenklige Dreiecke aufteilen lässt.Der Flächeninhalt einer Raute entspricht der Summe der Flächeninhalte dieser Dreiecke.
Das Drachenviereck: Eigenschaften, Umfang und Flächeninhalt
Bei einem Drachenviereck (auch Deltoid genannt) sind paarweise zwei einander anliegende Seiten gleich lang und die Diagonalen schneiden sich im rechten Winkel zueinander.
Das Drachenviereck findest du in dem Haus der Vierecke in der Reihe mit den grünen Figuren, unterhalb der Raute und des Rechtecks, ganz links.
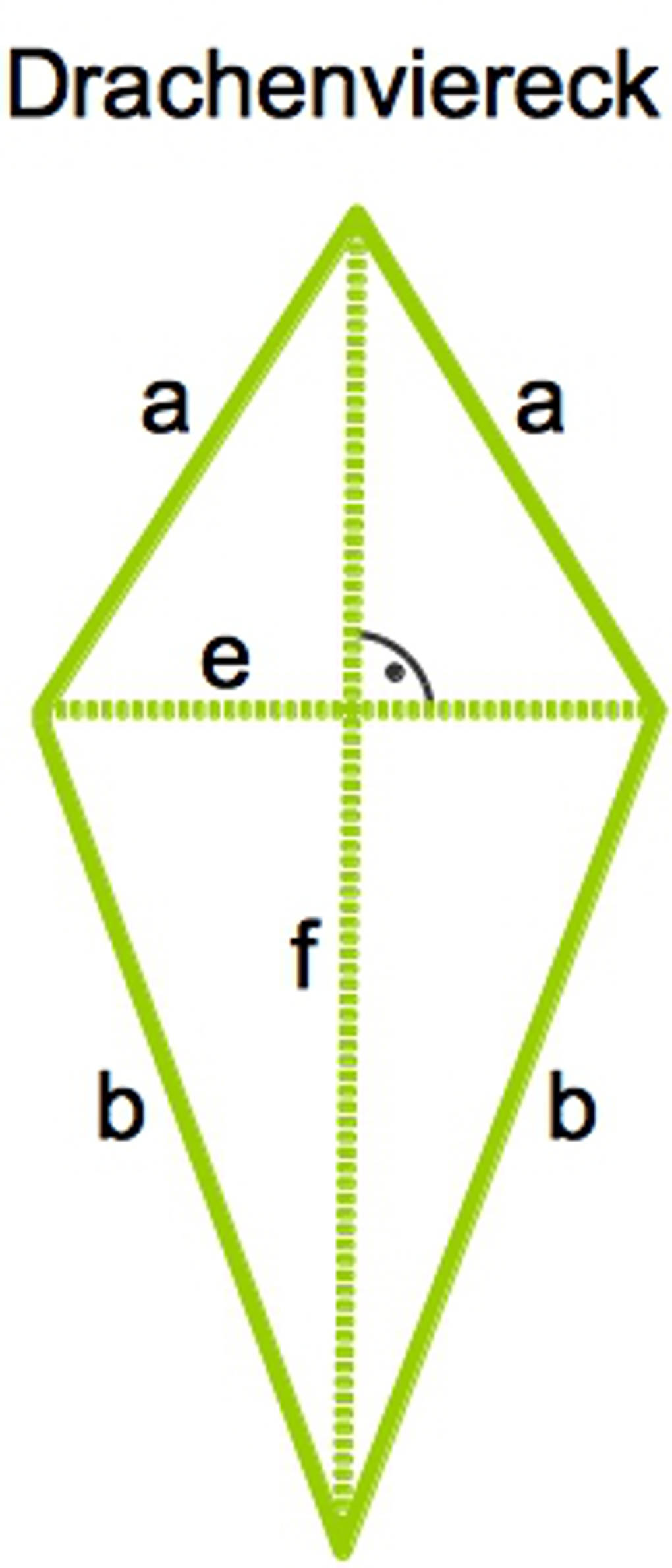
Eigenschaften Drachenviereck
- Die Diagonalen schneiden sich in einem rechten Winkel.
- Die paarweise aneinanderliegende Seiten sind gleich lang.
Ein Drachenviereck hat nur eine Symmetrieachse. Auf dieser liegt in dem dargestellten Drachenviereck die Diagonale $f$. Bei der Raute sind beide Diagonalen Symmetrieachsen.
Eine Raute ist auch ein Drachenviereck.
- Ein Drachenviereck muss keine Raute sein.
Umfang eines Drachenvierecks
In einem Drachenviereck sind jeweils zwei Seiten gleich lang. Der Umfang eines Drachenvierecks mit Seitenlängen $a$ und $b$ ist gegeben mit:
$u=a+a+b+b=2(a+b)$.
Der Flächeninhalt eines Drachenvierecks
Das Drachenviereck besteht aus zwei gleichschenkligen Dreiecken. Damit ist der Flächeninhalt des Drachenvierecks die Summe der Flächeninhalte der beiden gleichschenkligen Dreiecke.
Der Flächeninhalt jedes der beiden Dreiecke berechnet sich als Produkt von Grundseite und Höhe dividiert durch $2$.
Die Höhe des oberen Dreiecks $A_{\Delta_o}$ sei $h$, dann beträgt zugehörige Flächeninhalt:
$A_{\Delta_o}=\frac{e\cdot h}2$.
Die Höhe des unteren Dreiecks $A_{\Delta_u}$ beträgt $f-h$ und der zugehörige Flächeninhalt ist:
$A_{\Delta_u}=\frac{e\cdot (f-h)}2$.
Addierst du nun die beiden Flächeninhalte, so erhältst du den Flächeninhalt des Drachenvierecks:
$A=A_{\Delta_o}+ A_{\Delta_u}=\frac{e\cdot h}2+\frac{e\cdot (f-h)}2=\frac{e\cdot h+e\cdot (f-h)}{2}=\frac{e\cdot f}2$.
Der Flächeninhalt $A$ eines Drachenvierecks ist also gegeben durch
$A=\frac{e\cdot f}2$.
Anwendungsbeispiel Flächeninhalt Drachenviereck
Du möchtest mit deinen gefunden Stöcken und Stoff einen Drachen basteln.
Der längere Stock $f$ ist doppelt so lang wie der kürzere Stock $e$ mit $40~ \text{cm}$. Damit gilt $f=2\cdot e$. Wie viel Stoff benötigst du für deinen Drachen?
Wir verwenden die Formel zur Berechnung des Flächeninhalts eines Drachenvierecks. Die Stöcke $e$ und $f$ entsprechen den Diagonalen des Drachenvierecks.
$A=\frac{e\cdot f}{2}=\frac{e\cdot 2\cdot e}{2}=e^2=40 ~\text{cm}^{2}=1600~\text{cm}^2$.
Um deinen Drachen zu basteln benötigst du $1600~\text{cm}^2$ Stoff.
Alle Videos zum Thema
Videos zum Thema
Flächeninhalt und Umfang von Drachenvierecken und Rauten (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Flächeninhalt und Umfang von Drachenvierecken und Rauten (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal




 Flächeninhalt und Umfang von Rauten und Drachenvierecken
Flächeninhalt und Umfang von Rauten und Drachenvierecken









