Harmonische Teilung einer Strecke
- Harmonische Teilung einer Strecke – Erklärung
- Harmonische Teilung einer Strecke – Vorgehen
- Harmonische Teilung einer Strecke – vorgegebenes Verhältnis
- Harmonische Teilung einer Strecke – Punkt $S$ gegeben
- Harmonische Teilung einer Strecke – Punkt $T$ gegeben
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Harmonische Teilung einer Strecke
Harmonische Teilung einer Strecke – Erklärung
Eine Strecke $\overline{AB}$ kann auf verschiedene Arten geteilt werden. Du kannst zum Beispiel eine Strecke halbieren, indem du den Mittelpunkt einer Strecke berechnest oder eine Strecke in mehrere gleiche Teile teilst.
Außerdem wird zwischen der inneren Teilung einer Strecke und der äußeren Teilung einer Strecke unterschieden.
Die harmonische Teilung ist eine besondere Art der Teilung, in der eine Strecke $\overline{AB}$ innen durch einen Punkt $S$ im gleichen Verhältnis geteilt wird wie außen durch einen Punkt $T$.
Es gilt:
$\overline{AS} : \overline{SB} = \overline{AT} : \overline{TB}$
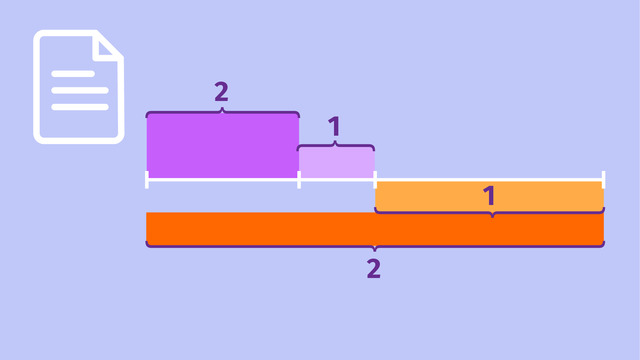
Die Strecke $\overline{AT}$ kann zum Beispiel doppelt so lang sein wie die Strecke $\overline{TB}$, sie stehen damit im Verhältnis $2:1$. Liegt eine harmonische Teilung vor, ist die Strecke $\overline{AS}$ dann auch doppelt so lang wie die Strecke $\overline{SB}$ – das Verhältnis ist hier ebenfalls $2 :1$.
Harmonische Teilung einer Strecke – Vorgehen
Das Vorgehen bei der harmonischen Teilung einer Strecke unterscheidet sich abhängig davon, ob ein Verhältnis oder einer der Punkte $S$ oder $T$ gegeben sind.
Harmonische Teilung einer Strecke – vorgegebenes Verhältnis
Wenn du eine Strecke $\overline{AB}$ nach einem vorgegebenen Verhältnis harmonisch teilen sollst, zum Beispiel im Verhältnis $3 : 1$, kannst du zuerst die innere Teilung vornehmen. Dafür konstruierst du zwei parallele Hilfslinien von den Punkten $A$ und $B$ aus auf die jeweils gegenüberliegende Seite von $\overline{AB}$. Auf diesen trägst du gleich große Teilstücke ab (z. B. mit dem Zirkel) und verbindest die jeweils äußersten für das innere Teilungsverhältnis $3:1$, das durch den Punkt $S$ gegeben ist.
Dieses Verfahren wendest du dann auch für die äußere Teilung an. Dafür verlängerst du die Hilfsparallele an Punkt $B$ auf die andere Seite und trägst dort ein gleich großes Teilstück ab. Dann verbindest du auch hier die äußersten Markierungen und erhältst so einen Schnittpunkt mit der Verlängerung von $\overline{AB}$ – Punkt $T$, der das äußere Teilungsverhältnis von $3:1$ gewährleistet.
Harmonische Teilung einer Strecke – Punkt $S$ gegeben
Wenn der Punkt $S$, der die Strecke im inneren Verhältnis teilt, gegebenen ist und du den Punkt $T$ konstruieren möchtest, der die Strecke im äußeren Verhältnis teilt, gehst du wie folgt vor:
- Zeichne zwei Hilfsparallelen auf der entgegengesetzten Seite der Geraden ein, die durch die Punkte $A$ und $B$ verlaufen.
- Zeichne eine Gerade durch den Punkt $S$, die die beiden Hilfsparallelen schneidet.
- Nenne die Schnittpunkt $C$ und $D$.
- Verlängere die zweite Hilfsparallele und trage den Abstand zwischen den Punkten $D$ und $B$ mit einem Zirkel auf der anderen Seite der Geraden noch einmal ab und nenne den neuen Punkt $D’$.
- Zeichne eine Gerade durch die Punkte $C$ und $D’$ und verlängere sie, bis du den Punkt $T$ erhältst, der als Schnittpunkt mit der ursprünglichen Geraden die Strecke $\overline{AB}$ im äußeren Verhältnis teilt.
Dieses Vorgehen funktioniert, da nach den Strahlensätzen Folgendes gilt:
$\overline{AT} : \overline{TB} = \overline{AC} : \overline{BD’}$
Da $\overline{BD’}=\overline{BD}$ gilt, gilt auch:
$\overline{AT} : \overline{TB} = \overline{AC} : \overline{BD}$
Für $\overline{AC} : \overline{BD}$ gilt wiederum wegen des Strahlensatzes:
$\overline{AC} : \overline{BD}=\overline{AS} : \overline{SB}$
Daher gilt insgesamt:
$\overline{AT} : \overline{TB} = \overline{AS} : \overline{SB}$
Das innere Teilungsverhältnis entspricht dem äußeren Teilungsverhältnis.
Harmonische Teilung einer Strecke – Punkt $T$ gegeben
Wenn der Punkt $T$, der die Strecke im äußeren Verhältnis teilt, gegebenen ist und du den Punkt $S$ konstruieren möchtest, der die Strecke im inneren Verhältnis teilt, gehst du wie folgt vor:
- Zeichne zwei Hilfsparallelen auf der gleichen Seite der Geraden ein, die durch die Punkte $A$ und $B$ verlaufen.
- Ziehe vom Punkt $T$ aus eine Gerade, die beide Hilfsparallelen schneidet.
- Nenne die Schnittpunkte $C$ und $D$.
- Verlängere die zweite Hilfsparallele und trage den Abstand zwischen den Punkten $B$ und $D$ mit einem Zirkel auf der anderen Seite der Geraden noch einmal ab und nenne den neuen Punkt $D’$.
- Verbinde die Punkte $C$ und $D’$, um den gesuchten Punkt $S$ zu erhalten, der als Schnittpunkt mit der ursprünglichen Geraden die Strecke $\overline{AB}$ im inneren Verhältnis teilt.
Harmonische Teilung einer Strecke – Zusammenfassung
Bei der harmonischen Teilung einer Strecke $\overline{AB}$ wird die Strecke durch einen Punkt $S$ innen im gleichen Verhältnis geteilt wie außen durch einen Punkt $T$.
Es gilt:
$\overline{AS} : \overline{SB} = \overline{AT} : \overline{TB}$
Du kannst die harmonische Teilung mit einem Geodreieck und einem Zirkel konstruieren, wenn das Teilungsverhältnis oder einer der Punkte $S$ oder $T$ gegeben sind.
9.711
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.787
Lernvideos
37.112
Übungen
32.540
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung





 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?