Prozentsatz, Prozentwert und Grundwert

Inhaltsverzeichnis zum Thema

• Prozentrechnung
• Gleichungen der Prozentrechnung
• Wie löst man eine Grundaufgabe? – erste Schritte für die Prozentrechnung
• Beispiele zur Prozentrechnung
• Lieblingsfach Mathematik – Aufgabe 1
• Bücherregal – Aufgabe 2
• Festival – Aufgabe 3
• Prozentuale Veränderung – Aufgabe
• Wachstumsrate und Wachstumsfaktor – Aufgabe
• Rabatte – Aufgabe
• Mehrwertsteuer – Aufgabe
• Kredite und Tilgung – Aufgabe
• Zinsrechnung – Aufgabe

Prozentrechnung

Die Prozentrechnung findet in vielen Bereichen Anwendung. Das Wort „Prozent“ kommt aus dem Lateinischen und heißt übersetzt „für Hundert“ oder „pro Hundert“. Prozentangaben werden also verwendet, um einen Anteil an einem Ganzen anzugeben. Wie rechnet man aber mit Prozentangaben? Wir wissen bereits, dass eine Prozentangabe, z. B. 99 % das 100-fache einer Dezimalzahl (Kommazahl), z. B. 0,99, ist. Möchte man eine Dezimalzahl in eine Prozentangabe verwandeln, multipliziert man die Dezimalzahl mit 100:

$0,99 \cdot 100 = 99\% $

Teilt man eine Prozentangabe mit 100, erhält man die Dezimalzahl:

$ \frac{99}{100} = 0,99$

In der Prozentrechnung gibt es vier Begriffe, die du unbedingt kennen solltest. Es handelt sich um folgende Größen:

• der Grundwert $\text{G}$
• die Prozentzahl $\text{p}$
• der Prozentwert $\text{W}$
• der Prozentsatz $\text{p}\%$

Der Zusammenhang dieser Größen wird durch folgende Formel für die Prozentrechnung beschrieben:

$\frac{\text{W}}{\text{G}}=\text{p}\%$

Diese Formel kann mithilfe von Äquivalenzumformungen umgestellt werden. Je nachdem, welche Größe du berechnen möchtest.

Gleichungen der Prozentrechnung

In einer Rechenaufgabe wird entweder der Grundwert, der Prozentsatz oder der (Prozent-)Wert gesucht. Um die gesuchte Angabe berechnen zu können, brauchst du eine der folgenden Gleichungen:

• $\text{G} = \frac{100 \cdot \text{W}}{\text{p}}$
• $\text{W}= \frac{p \cdot \text{G}}{100}$
• $\text{p} = \frac{100 \cdot \text{W}}{\text{G}}$
• $\text{p}\% = \frac{\text{W}}{\text{G}}$

Wie löst man eine Grundaufgabe? – erste Schritte für die Prozentrechnung

• Schritt 1: Lies die Aufgabe durch. Überlege, welche Informationen du dem Text entnehmen kannst: Kennst du $\text{G}$, $\text{W}$, $\text{p}\%$ oder $\text{p}$?
• Schritt 2: Nun weißt du, welche Angabe in der Aufgabe gesucht ist und welche Informationen gegeben sind. Schreibe sie heraus.
• Schritt 3: Überlege, welche Gleichung du brauchst, um die gesuchte Angabe zu berechnen.
• Schritt 4: Setze die dir bekannten Angaben in die Gleichung ein. Nun musst du sie nur noch lösen.

Beispiele zur Prozentrechnung

Um die Prozentrechnung einmal näher kennenzulernen, werden im Folgenden ein paar Grundaufgaben zur Prozentrechnung gerechnet. Bei den meisten Aufgaben sind jeweils zwei der drei Größen $\text{G}$, $\text{W}$ und $\text{p}\%$ bekannt und die dritte muss berechnet werden.

Lieblingsfach Mathematik – Aufgabe 1

$70\%$ der Kinder in der Klasse 8b mögen Mathematik. Die Gesamtzahl aller Schüler/-innen ist $30$. Wie viele Kinder mögen Mathematik?

Welche Werte sind bereits bekannt?

• Die Gesamtzahl der Kinder ist $\text{G}=30$.
• Der Prozentsatz ist $\text{p}\%=0,7$.

Gesucht ist also der Prozentwert $\text{W}$. Setzt man nun die bekannten Größen in die Formel ein und formt diese nach der gesuchten Größe $\text{W}$ um, so erhält man folgende Rechnung:

$\begin{array}{rcll} \frac{\text{W}}{30} &=& 0,7 &\vert \cdot 30 \\ \text{W} &=& 0,7\cdot 30 & \\ \text{W} &=& 21& \end{array}$

Insgesamt mögen also $21$ von $30$ Kindern in dieser Klasse Mathematik – da schlägt das Herz der Mathelehrerin bestimmt höher.

Bücherregal – Aufgabe 2

Luke wirft einen Blick in sein Bücherregal. Es sind insgesamt $120$ Bücher. Davon sind $30$ Comics. Wie hoch ist der Prozentsatz $\text{p}\%$?

Zunächst werden wieder die bekannten Größen in die Formel eingesetzt:

$\begin{array}{lll} \text{p}\% &=& \frac{30}{120} \\ \text{p}\% &=& 0,25 \end{array}$

$25 ~\%$ von Lukes Büchern sind Comics.

Auch mit dem Dreisatz ist die Bestimmung des gesuchten Prozentsatzes möglich.

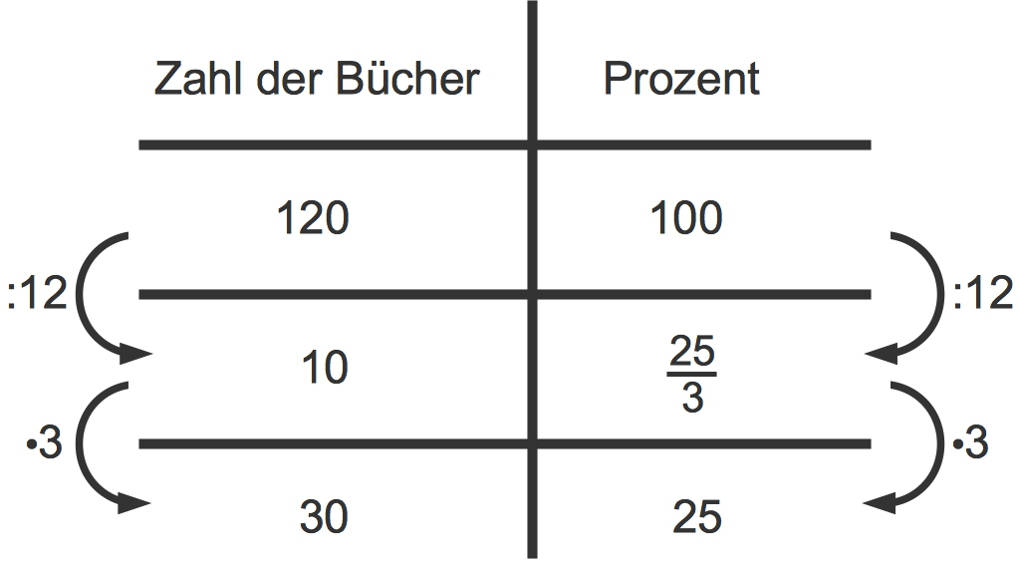
Du weißt, dass der Grundwert $100\%$ entspricht. Wie viel Prozent entspricht dann dem Prozentwert?

• Zuerst dividierst du $\text{G}=120$ durch $12$, um auf $10$ zu kommen. Dies entspricht $\frac{25}3\%$.
• Dann multiplizierst du mit $3$, um auf $\text{W}=30$ zu kommen. Dies entspricht $25\%$.

Die Prozentrechnung ist ein Beispiel für eine direkt proportionale Zuordnung. Direkt proportional bedeutet: Je mehr desto mehr.

Festival – Aufgabe 3

$130$ Besucher/-innen eines Festivals sind von außerhalb angereist: Das sind $20~\%$. Wie viele Besucher/-innen befinden sich auf dem Festival? $\text{W}$ und $\text{p}\%$ sind bekannt, $\text{G}$ wird gesucht.

$\begin{array}{rcll} 0,2 &=& \frac{130}{G} & \vert \cdot \text{G} \\ 0,2\cdot \text{G} & = & 130 & \vert :0,2 \\ \text{G} & = & 650 & \end{array}$

Insgesamt befinden sich also $\text{G}=650$ Besucher/-innen auf dem Festival.

Prozentuale Veränderung – Aufgabe

Herr Kopp hat eine Lohnerhöhung erhalten. Vor der Lohnerhöhung hat er $3500~€$ erhalten und danach $3700~€$. Die prozentuale Veränderung lässt sich mithilfe folgender Formel berechnen:

$ \text{p}\%=\frac{\text{Wert}_{\text{neu}}-\text{Wert}_{\text{alt}}}{\text{Wert}_{\text{alt}}}=\frac{3700~€-3500~€}{3500~€}\approx 5,7~\% $

Wachstumsrate und Wachstumsfaktor – Aufgabe

Ein Wald wird neu aufgeforstet. Dadurch wird die gesamte Fläche des Waldes von Jahr zu Jahr um $5\%$ größer. Wie groß ist die Fläche nach einem Jahr oder nach fünf Jahren, wenn die anfängliche Fläche $10~\text{ha}$ beträgt?

• Die Wachstumsrate ist $\text{p}\%=0,05$.
• Der Wachstumsfaktor ergibt sich zu $1+\text{p}\%=1,05$.

Somit kannst du die Wachstumsfunktion wie folgt aufschreiben:

$\text{A}(t)=10\cdot 1,05^t$

Dabei ist $t$ die Zeit in Jahren und $A(t)$ die Waldfläche nach $t$ Jahren.

• $A(1)=10\cdot 1,05=10,5~\text{ha}$ beschreibt die Waldfläche nach $1$ Jahr.
• $A(5)=10\cdot 1,05^5\approx 12,76~\text{ha}$ beschreibt die Waldfläche nach $5$ Jahren.

Rabatte – Aufgabe

Paula möchte sich eine neue Jeans kaufen. Eine Jeans, die sie sich ausgesucht hat, kostet $80~€$. Heute gibt es auf jeden Artikel $15\%$ Rabatt. Wie viel kostet die Jeans jetzt?

• Zuerst rechnet Paula aus, wie viel $15\%$ Rabatt von $80~€$ sind: $\text{W}=0,15\cdot 80~€=12~€$.
• Nun kann sie die $12~€$ abziehen: $80~€-12~€=68~€$.

Paula muss für die Hose $68~€$ bezahlen.

Mehrwertsteuer – Aufgabe

Die Mehrwertsteuer, abgekürzt MwSt, wurde am 1. Januar 1968 eingeführt. Unternehmen addieren zu dem Nettobetrag die Mehrwertsteuer. Dieser neue Betrag heißt Bruttobetrag. Du hast vielleicht auf Rechnungen schon einmal die Mehrwertsteuer gesehen. Dabei ist dir vielleicht auch aufgefallen, dass es sowohl $7\%$ als auch $19\%$ Mehrwertsteuer gibt. Das hängt von der entsprechenden Ware oder Arbeit ab.

Die Firma Farbenfroh streicht das Haus der Familie Glasbachtal.

Der Nettobetrag der Rechnung beträgt $2500~€$. Die Chefin der Firma Farbenfroh erinnert sich, dass sie ja noch die Mehrwertsteuer mit 19 % berechnen muss. Diese muss sie noch zur Rechnung hinzufügen.

• $\text{G}\cdot p\%=2500~€\cdot 0,19=475~€$. Dies ist der Mehrwertsteuerbetrag.
• $2500~€+475~€=2975~€$. Dies ist der Bruttobetrag, den Familie Glasbachtal zahlen muss.

Kredite und Tilgung – Aufgabe

Familie Glasbachtal möchte auch noch das Dach ihres Hauses neu decken lassen. Die Gesamtkosten betragen $12000~€$. Dafür müssen sie einen Kredit aufnehmen.

Sie müssen der Bank Zinsen in Höhe von $7,9\%$ bezahlen. Monatlich können sie eine Rate von $350~€$ bezahlen. Der Sachbearbeiter der Bank erstellt einen Tilgungsplan für den Kredit. Diesen kannst du hier für die ersten zwei Monate sehen:

1. Zum Ende des ersten Monats fallen Zinsen in Höhe von $12000~€\cdot \frac{7,9}{12\cdot 100}=79~€$ an. Die Rate beträgt $350~€$. Die Tilgung eines Kredites berechnet sich durch die Differenz aus Rate und Zinsen: $350~€-79~€=271~€$. Wenn man diesen Betrag von der Kreditsumme subtrahiert, erhält man die Restschuld: $12000~€-271~€=11729~€$.

2. Zum Ende des zweiten Monats fallen wieder Zinsen an. Diese werden natürlich nur auf die Restschuld angerechnet: $11729~€\cdot \frac{7,9}{12\cdot 100}=77,22~€$. Die Tilgung beträgt dann $350~€-77,22~€=272,78~€$. Dies wird wieder von der Restschuld abgezogen, um zur neuen Restschuld zu gelangen: $11729~€-272,78~€=11456,22~€$.

Zinsrechnung – Aufgabe

Ein Spezialfall der Prozentrechnung ist die Zinsrechnung. Immer wenn du Geld auf dein Sparbuch legst oder dir Geld von einer Bank leihst, spielen Zinsen eine wichtige Rolle. Es gibt im Grunde keinen Unterschied zur oben beschriebenen Prozentrechnung. Es werden allerdings andere, wirtschaftliche Begriffe verwendet:

• Der Grundwert aus der Prozentrechnung heißt hier Kapital $\text{K}$, Guthaben oder Kredit.
• Der Prozentwert heißt in der Zinsrechnung Zinsen $\text{Z}$.
• Der Prozentsatz entspricht dem Zinssatz $\text{p}\%$.