Koordinatensysteme
In einem Koordinatensystem lassen sich geometrische Figuren und Punkte einfach darstellen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Koordinatensystem?
- Vom Zahlenstrahl zum Koordinatensystem
- Aufbau und Bezeichnung eines Koordinatensystems
- Punkte in einem Koordinatensystem
Was ist ein Koordinatensystem?
Ein Koordinatensystem, oder auch kurz KOS, dient zur Darstellung von Punkten oder anderen geometrischen Elementen in der Ebene. Du wirst sicherlich auch den Begriff des kartesischen Koordinatensystems hin und wieder hören. Dieser Name leitet sich von dem französischen Mathematiker René Descartes ab.
Vom Zahlenstrahl zum Koordinatensystem
Du kennst doch sicher noch einen Zahlenstrahl.
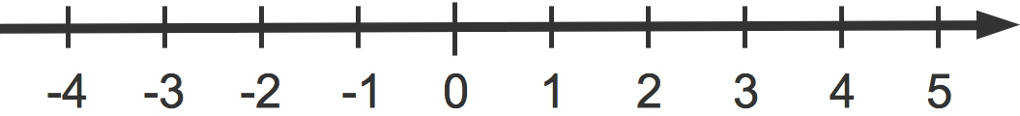
Auf einem Zahlenstrahl kannst du Zahlen eintragen. Hier sind die Zahlen von $-4$ bis $5$ zu erkennen. Der Abstand zwischen zwei Zahlen ist immer gleich groß. Eine Zahl wie $-3$ kannst du dort leicht einzeichnen.
Nur: Wie kannst du Zahlenpaare zeichnen? Was machst du, wenn du einen Punkt $P(2|3)$ zeichnen sollst? Auf einer Zahlengerade ist dies nicht möglich.
Punkte zeichnest du in einem Koordinatensystem.
Aufbau und Bezeichnung eines Koordinatensystems
Ein Koordinatensystem besteht aus
- einer waagerechten Achse, der x-Achse.
- einer senkrechten Achse, der y-Achse.
Die x-Achse sieht so aus wie der Zahlenstrahl, die y-Achse wie ein um 90° gedrehter Zahlenstrahl.
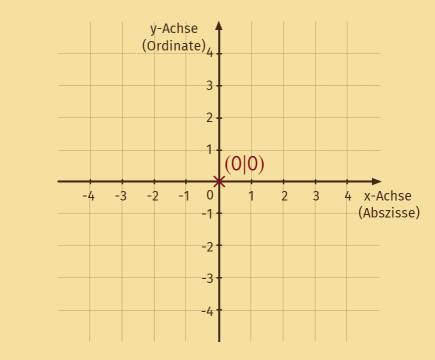
- Die x-Achse wird auch als Abszisse oder Rechtsachse bezeichnet.
- Die y-Achse wird auch als Ordinate oder Hochachse bezeichnet.
- Die beiden Koordinatenachsen schneiden sich in einem Punkt. Dies ist der Koordinatenursprung $O(0|0)$.
Koordinatensysteme zeichnen
Ebenso wie bei dem Zahlenstrahl müssen die Abstände zwischen den Zahlen auf den Achsen gleich groß sein.
Denke daran, die Koordinatenachsen zu beschriften:
- Rechts an die x-Achse zeichnest du einen Pfeil nach rechts und schreibst $x$ an diese Achse.
- Oben an die y-Achse zeichnest du einen Pfeil nach oben und schreibst $y$ an diese Achse.
- Unterteile die Achsen in regelmäßigen Abständen mit Strichen und schreibe die Zahlen daran.
Quadranten
Ein Koordinatensytem wird in vier Quadranten unterteilt. Diese beginnen oben rechts und sind gegen den Uhrzeigersinn bezeichnet:
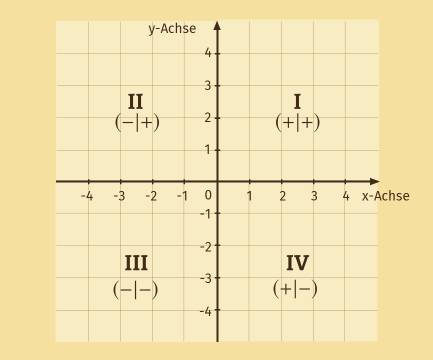
In den vier Quadranten gilt:
- Im I. Quadranten ist sowohl $x \gt 0$ als auch $y \gt 0$.
- Im II. Quadranten ist $x \lt 0$ und $y \gt 0$.
- Im III. Quadranten ist sowohl $x \lt 0$ als auch $y \lt 0$.
- Im IV. Quadranten ist $x \gt 0$ und $y \lt 0$.
Die Punkte auf den Koordinatenachsen werden keinem Quadranten zugeordnet, da eine ihrer Koordinaten den Wert $0$ hat.
Punkte in einem Koordinatensystem
Wenn du ein Koordinatensystem in dein Heft gezeichnet hast, kannst du zum Beispiel Punkte in dieses Koordinatensystem eintragen. Wie das geht, siehst du hier.
Punkte in ein Koordinatensystem eintragen
Was ist ein Punkt? Ein Punkt ist ein geordnetes Zahlenpaar $(x|y)$. Hier erkennst du sicher schon die Bezeichnungen der Koordinatenachsen. Die erste Koordinate eines Punktes ist also die x-Koordinate und die zweite die y-Koordinate.
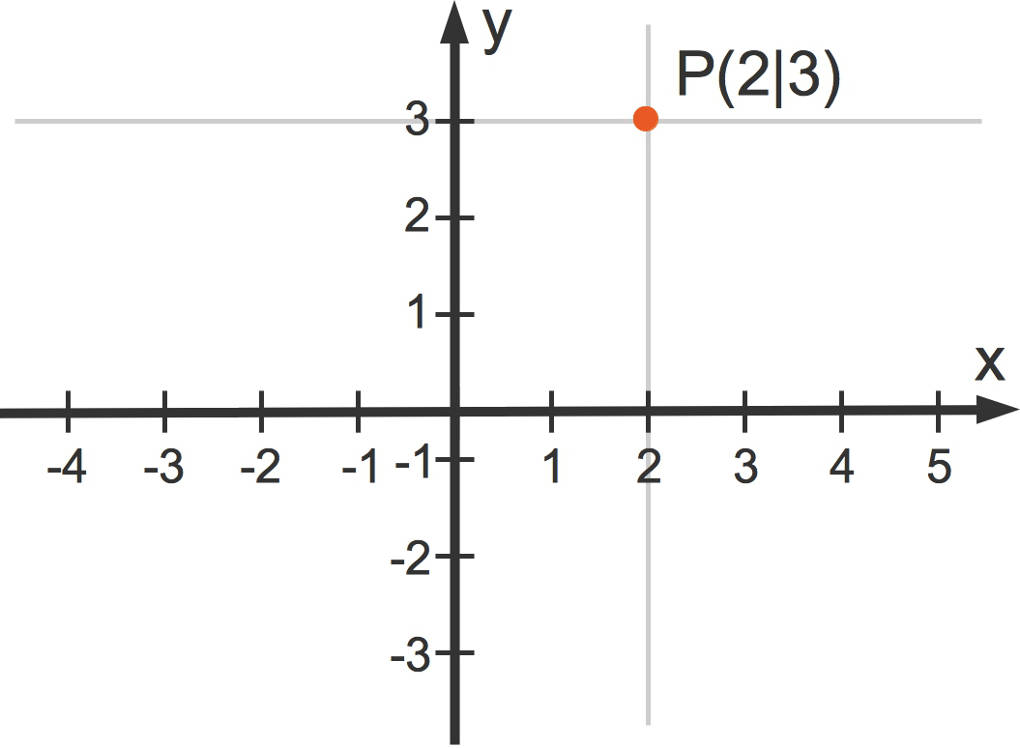
Zum Beispiel hat der Punkt $P(2|3)$ die x-Koordinate $x=2$ und die y-Koordinate $y=3$.
Um diesen Punkt in ein Koordinatensystem einzutragen, gehst du wie folgt vor:
- Du zeichnest eine zur y-Achse parallele Linie durch $x=2$.
- Nun zeichnest du eine zur x-Achse parallele Linie durch $y=3$.
- Diese beiden Linien schneiden sich in einem Punkt. Dies ist der Punkt $P(2|3)$.
Dies kannst du hier sehen.
Punkte aus einem Koordinatensystem ablesen
Ebenso kannst die Koordinaten eines Punktes aus einem Koordinatensystem ablesen.
- Du zeichnest von dem Punkt ausgehend eine zur y-Achse parallele Linie. Dort, wo diese Linie die x-Achse schneidet, kannst du die x-Koordinate ablesen.
- Nun zeichnest du eine zur x-Achse parallele Linie. Diese schneidet die y-Achse. Hier kannst du die y-Koordinate des Punktes ablesen.
Probiere dies mal mit dem Punkt $P$:
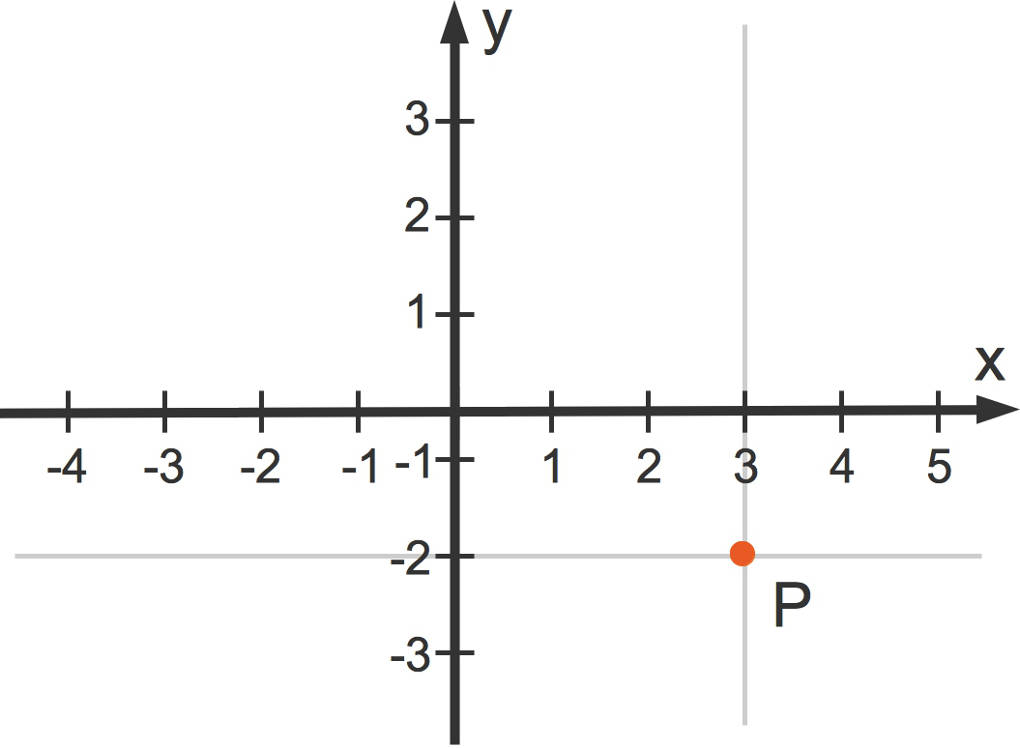
Hast du die Koordinaten erkannt? Der Punkt $P(3|-2)$ hat die x-Koordinate $x=3$ und die y-Koordinate $y=-2$.
Alle Videos zum Thema
Videos zum Thema
Koordinatensysteme (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Koordinatensysteme (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen








 Koordinatensystem – Einführung
Koordinatensystem – Einführung
 Koordinatensystem – Aufbau
Koordinatensystem – Aufbau
 Koordinatensystem – Einzeichnen und Ablesen von Punkten
Koordinatensystem – Einzeichnen und Ablesen von Punkten
 Koordinatensystem – Einzeichnen und Ablesen von Punkten (Übungsvideo)
Koordinatensystem – Einzeichnen und Ablesen von Punkten (Übungsvideo)









