Zentrische Streckung
Längenverhältnis, Maßstab, Vergrößerungsfaktor, Ähnlichkeit, vergrößern, verkleinern, ähnliche Figuren, Streckfaktor, Streckzentrum, Streckfaktor quadrieren
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine zentrische Streckung?
- Zentrische Streckung von Strecken
- Zentrische Streckung von Vielecken
Was ist eine zentrische Streckung?
Eine zentrische Streckung ist eine Ähnlichkeitsabbildung.
Für eine zentrische Streckung benötigst du:
- ein Streckzentrum (einen Punkt) $Z$ sowie
- einen Streckfaktor
Hier siehst du, wie eine zentrische Streckung von einem Punkt, $A$, durchgeführt wird.
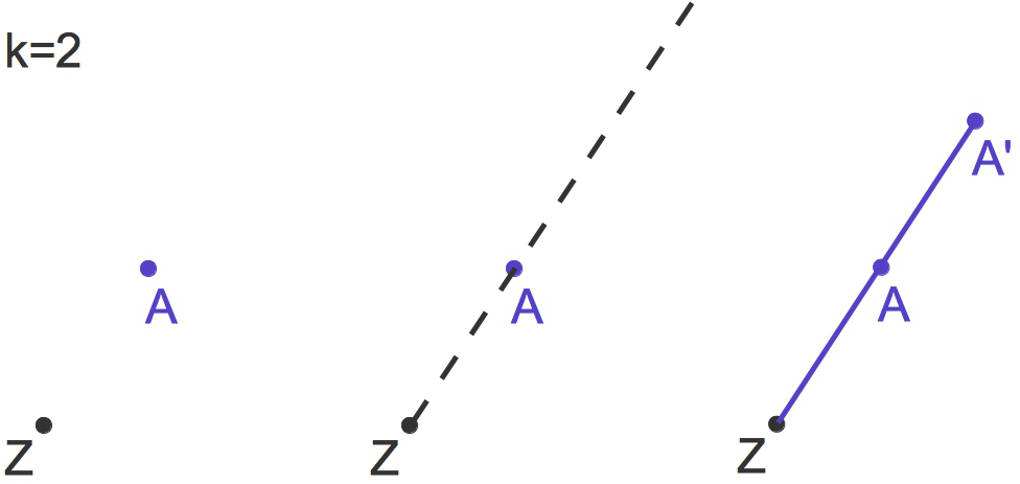
- Gegeben ist das Streckzentrum $Z$ und der Streckfaktor $k=2$ sowie ein Punkt $A$.
- Zunächst zeichnest du eine Halbgerade von $Z$ durch $A$.
- Dann misst du den Abstand von $Z$ zu $A$.
- Diesen Abstand multiplizierst du mit dem Streckfaktor, hier $k=2$, und trägst von $Z$ aus eine Strecke mit der Länge des doppelten Abstandes ab.
- Am Ende dieser Strecke befindet sich der Bildpunkt $A'$ des Originalpunktes $A$.
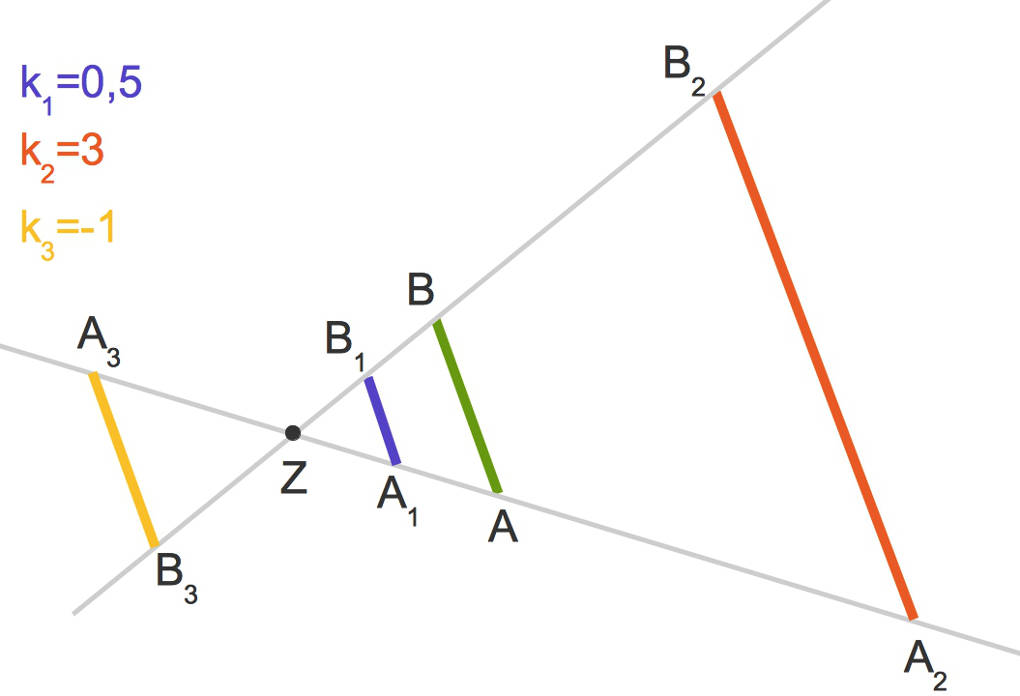
Zentrische Streckung von Strecken
Du erhältst die zentrische Streckung einer Strecke, indem du zu den beiden Endpunkten der Strecke wie oben beschrieben die Bildpunkte bestimmst. Die Verbindung dieser Bildpunkte ist die zentrisch gestreckte Strecke.
Dabei gelten die folgenden Eigenschaften:
- Die Originalstrecke, hier grün, und alle Bildstrecken sind parallel zueinander.
- Die Bildstrecke ist exakt $|k|$ mal so lang wie die Originalstrecke.
- Für alle $|k|<1$, zum Beispiel die blaue Strecke, wird die Bildstrecke verkleinert und für alle $|k|>1$, zum Beispiel die rote Strecke, wird die Bildstrecke vergrößert.
- Bei negativem $k$, hier die gelbe Bildstrecke, wird die Strecke an dem Streckzentrum gespiegelt. Beachte, dass dabei die Anordnung der Punkte umgekehrt wird.
Zentrische Streckung von Vielecken
An dem Beispiel eines Parallelogramms siehst du hier die zentrische Streckung eines Vielecks. Das Original ist grün gestrichelt dargestellt. Die zentrische Streckung wird für jeden der Eckpunkte wie oben beschrieben durchgeführt. Zuletzt werden die Bildpunkte miteinander zu dem grünen Bildparallelogramm verbunden.
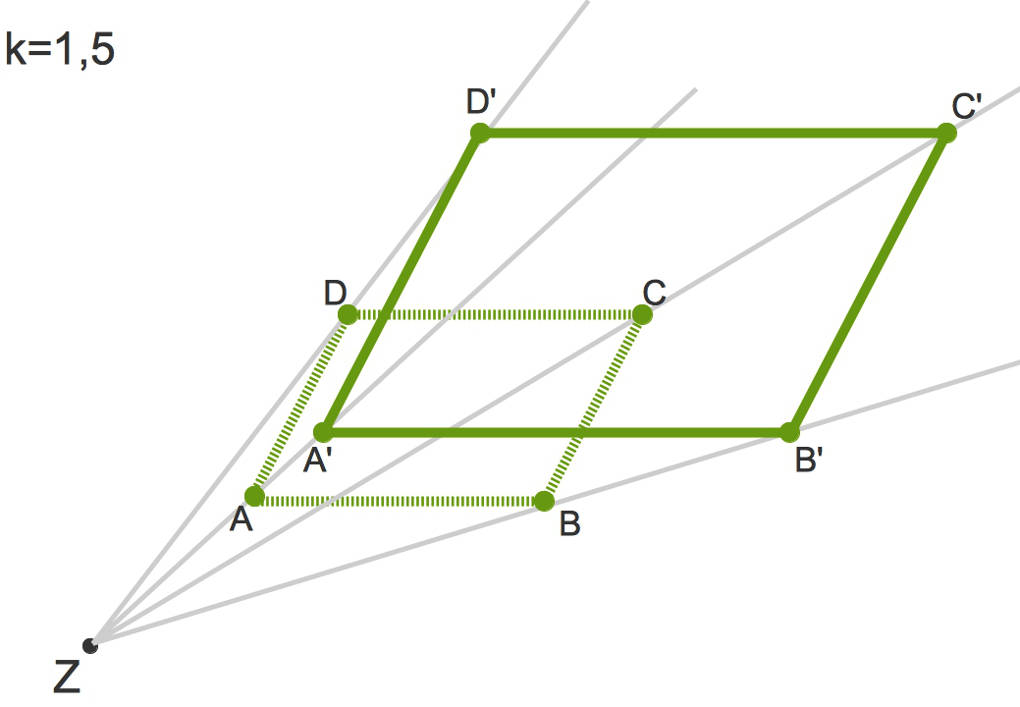
Auch hier kannst du erkennen, dass
- Originalstrecke und Bildstrecke parallel zueinander sind,
- die Längenverhältnisse der Seiten zueinander überein stimmen sowie
- die einander entsprechenden Winkel gleich groß sind
Das bedeutet, dass das Original und das Bild bei einer zentrischen Streckung ähnlich zueinander sind. Im Allgemeinen ist eine zentrische Streckung keine Kongruenzabbildung. Eine solche liegt bei Verschiebungen, Drehungen, Achsenspiegelungen sowie Punktspiegelungen vor.
Für $k=1$ oder $k=-1$ ist eine zentrische Streckung auch eine Kongruenzabbildung.
Du kannst zentrische Streckungen für beliebige Figuren durchführen.
Wenn du zum Beispiel einen Kreis zentrisch strecken sollst, gehst du wie folgt vor:
- Zuerst führst du die zentrische Streckung eines Punktes mit dem Mittelpunkt des Kreises durch.
- Der Radius des Originalkreises wird mit $|k|$ multipliziert.
- Zuletzt zeichnest du einen Kreis um den Bildpunkt des Mittelpunktes mit dem multiplizierten Radius. So erhältst du den Bildkreis.
Alle Videos zum Thema
Videos zum Thema
Zentrische Streckung (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Zentrische Streckung (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal







 Zentrische Streckung – positiver Streckfaktor
Zentrische Streckung – positiver Streckfaktor
 Zentrische Streckung – negativer Streckfaktor
Zentrische Streckung – negativer Streckfaktor
 Umkehrung der zentrischen Streckung – Streckzentrum und Streckfaktor bestimmen
Umkehrung der zentrischen Streckung – Streckzentrum und Streckfaktor bestimmen









