Permutation
Einfach lernen mit Videos, Übungen, Aufgaben & Arbeitsblättern
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Permutation?
Stelle dir vor, du hast drei Kugeln, eine blaue, eine grüne und eine rote. Wie viele verschieden Möglichkeiten gibt es, diese drei Kugeln in eine Reihe zu legen?
- Wir fangen zum Beispiel ganz links mit der blauen an, dann könnte die grüne und dann die rote Kugel kommen. Es könnte aber auch zuerst die rote und dann die grüne Kugel kommen.
- Natürlich könnte auch die grüne oder die rote Kugel ganz links liegen.
- Schauen wir uns das einmal als Bild an:

Du kannst hier sehen, dass es sechs verschiedene Anordnungen der drei Kugeln gibt. Jede dieser Anordnung heißt Permutation. Dieses Wort kommt von dem lateinischen Wort „permutare“ für „vertauschen“.
Wenn du nun wissen willst, wie viele Anordnungen es bei $20$ oder $30$ oder noch mehr Kugeln gibt, wärst du ziemlich lange beschäftigt, wenn du alle Anordnungen probieren würdest.
Definition
Jede mögliche Anordnung von $n$ Elementen, in der jedes dieser $n$ Elemente verwendet wird, heißt Permutation dieser Elemente.
Dabei müssen die folgenden Punkte berücksichtigt werden:
- Die $n$ Elemente der Ausgangsmenge unterscheiden sich voneinander.
- Jedes Element muss in der Permutation vorkommen.
- Keines der Elemente darf mehrmals vorkommen.
Berechnen der Anzahl aller Permutationen
Schauen wir uns noch einmal das Beispiel mit den drei Kugeln an. Die Anzahl aller Permutationen dieser drei Kugeln ist $P_3=6$. Diese Anzahl kannst du auch rechnerisch herleiten, ohne die Kugeln hinlegen zu müssen:
- Für die erste Position gibt es drei Kugeln, die du dorthin legen kannst.
- Wenn auf der ersten Position bereits eine Kugel liegt, gibt es für die zweite noch zwei ($2=3-1$) Möglichkeiten.
- Zusammen sind dies bereits $3\cdot 2$, also $6$ Möglichkeiten.
- Nun liegen bereits auf den ersten beiden Positionen zwei Kugeln. Es bleibt für die letzte Position nur noch eine Kugel übrig.
- Schließlich multiplizierst du $3\cdot 2\cdot 1=6$.
- Dies ist gerade die Anzahl aller Permutationen von drei Elementen.
Für ein Produkt der Form $[n \cdot (n-1) \cdot \ldots \cdot (n-n)]$, also zum Beispiel $3\cdot 2\cdot1$, gibt es auch einen Namen. Man nennt ein solches Produkt auch Fakultät. Am Taschenrechner ist das die Taste mit einem Ausrufezeichen „!“.
Ganz allgemein ist die Anzahl aller Permutationen einer $n$-elementigen Menge gegeben durch:
$P_n=n!$
Beispiele
- $4!=4\cdot 3\cdot 2\cdot 1=24$
- $5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120$
- Übrigens $5!=5\cdot 4!=5\cdot 24=120$
- Ganz allgemein gilt: $n!=n\cdot (n-1)\cdot (n-2)\cdot ... \cdot 2\cdot 1$ oder
- $n!=n\cdot (n-1)!$
Permutationen ohne Zurücklegen
Eine Permutation ohne Zurücklegen oder auch "Permutation ohne Wiederholungen" entspricht der oben angegeben Definition.
Permutationen werden im Zusammenhang mit der Kombinatorik, einem Teilgebiet der Stochastik, betrachtet.
Die Kombinatorik beschäftigt sich mit
- der Bestimmung der Anzahl möglicher Anordnungen, wie zum Beispiel den Permutationen, oder
- dem Auswählen von unterscheidbaren oder nicht unterscheidbaren Elementen.
Dabei unterscheidet man zwischen Zufallsversuchen „ohne Zurücklegen“ ("ohne Wiederholungen") und „mit Zurücklegen“ ("mit Wiederholungen") sowie „unter Berücksichtigung der Reihenfolge“ und „ohne Berücksichtigung der Reihenfolge“.
Dies ist wichtig für das Berechnen von Wahrscheinlichkeiten, zum Beispiel Laplace-Wahrscheinlichkeiten.
Eine Permutation ohne Zurücklegen kannst du verstehen als einen Zufallsversuch „ohne Zurücklegen“ und „unter Berücksichtigung der Reihenfolge“.
Beispiel

Pauls Familie möchte ein Familienfoto machen lassen.
- Zu der Familie gehören fünf Erwachsene (Oma, Opa, Pauls Eltern und seine Tante) sowie
- sechs Kinder (seine beiden Geschwister und seine drei Cousinen und Cousins).
Die Erwachsenen stehen in der hinteren Reihe und die Kinder in der vorderen.
Wie viele Möglichkeiten gibt es für das Aufstellen der Erwachsenen? Dies sind: $P_5=5!=120$.
- Wie viele Möglichkeiten gibt es für das Aufstellen der Kinder? Dies sind: $P_6=6!=720$.
- Wie viele Möglichkeiten gibt es insgesamt, die einzelnen Familienmitglieder aufzustellen? Hierfür musst du die beiden bereits bekannten Ergebnisse multiplizieren: $120\cdot 720=86400$.
Da kann der Termin bei dem Fotografen schon etwas länger dauern. Aber vielleicht möchten Oma und Opa unbedingt nebeneinander stehen oder die jeweiligen Geschwister. Dann verändert sich auch die Anzahl.
Permutationen mit Zurücklegen
Auch hierfür schauen wir uns ein Beispiel an. In einer Urne befinden sich eine rote und eine blaue Kugel. Es wird dreimal gezogen. Natürlich wird die bereits gezogene Kugel wieder zurück gelegt.
Die möglichen Permutationen kannst du dir mit Hilfe eines Baumdiagramms klarmachen:
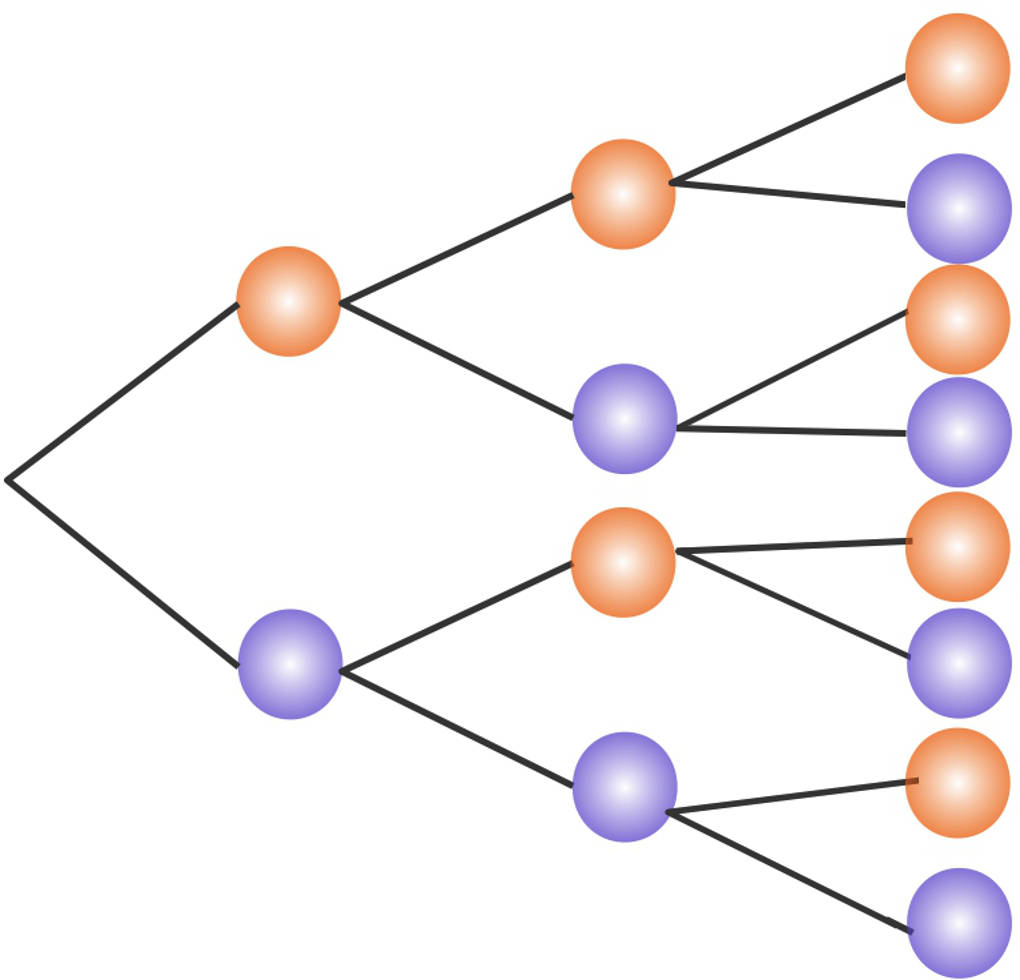
Du siehst, dass eine Kugel auch mehrmals vorkommen kann. Insgesamt gibt es $8=2^3$ verschiedene Anordnungen der beiden Farben der Kugeln.
Nun kannst du dich fragen, wie viele Anordnungen es gibt, in denen, zum Beispiel, zwei rote und eine blaue Kugel vorkommen. Dies kannst du dir an dem Baumdiagramm anschauen. Es gibt drei solcher Anordnungen:
$(r|r|b)$, $(r|b|r)$ und $(b|r|r)$.
Auch hier ist klar, dass eine Untersuchung mit Kugeln oder mit Hilfe eines Baumdiagramms sehr umfangreich werden kann.
Um die Anzahl der Möglichkeiten zu berechnen, kannst du die folgende Formel verwenden:
$\quad~~~^W P_n=\frac{n!}{n_1!\cdot n_2!\cdot ... \cdot n_k!}$.
- Dabei ist $n$ die Anzahl der Durchführungen des Experimentes, zum Beispiel die Häufigkeit des Ziehens.
- $n_1$, ..., $n_k$ entsprechen den Häufigkeiten des Auftretens eines Merkmals.
- $~^W$ steht für "mit Wiederholungen" / "mit Zurücklegen".
- Es gilt: $n_1+n_2+...+n_k=n$.
Beispiel 1
Bei dem obigen Beispiel bedeutet dies:
- $n=3$ entspricht der Anzahl an Durchführungen.
- $n_1=2$ entspricht der Häufigkeit des Auftretens einer roten Kugel.
- $n_2=1$ entspricht der Häufigkeit des Auftretens einer blauen Kugel.
Dann ist
$\quad~~~^W P_3=\frac{3!}{2!\cdot 1!}=\frac{6}{2}=3$.
Beispiel 2
Ein Zahlenschloss hat sieben Stellen. An drei dieser Stellen soll eine $1$, an zwei Stellen eine $5$ und an den übrigen zwei Stellen eine $6$ stehen. Wie viele Möglichkeiten gibt es, dieses Zahlenschloss einzustellen.
Zunächst machst du dir klar, was $n$, $n_1$, $n_2$ und $n_3$ jeweils ist:
- $n=7$ ist die Gesamtzahl der Stellen des Zahlenschlosses.
- $n_1=3$ entspricht der Häufigkeit des Auftretens der Zahl $1$.
- $n_2=2$ entspricht der Häufigkeit des Auftretens der Zahl $5$.
- $n_3=2$ entspricht der Häufigkeit des Auftretens der Zahl $6$.
Somit ist
$\quad~~~^W P_7=\frac{7!}{3!\cdot 2!\cdot 2!}=\frac{5040}{6\cdot 2\cdot 2}=210$.
Das sind doch noch recht viele Möglichkeiten: Also merke dir deine Zahlenkombination gut, ansonsten bist du ein wenig mit Probieren beschäftigt.
Alle Videos zum Thema
Videos zum Thema
Permutation (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Permutation (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal




 Permutationen und Fakultät
Permutationen und Fakultät









