Mittelwertsatz
stetige Funktionen, Mittelwertsatz der Differentialrechnung, Satz von Rolle
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Der Mittelwertsatz
- Die Voraussetzungen
- Die Aussage
- Der Mittelwertsatz anschaulich
- Ein Beispiel für die Verletzung einer Voraussetzung:
- Der Satz von Rolle
Der Mittelwertsatz
Der Mittelwertsatz ist ein Satz der Differentialrechnung, welche sich mit den Ableitungen von Funktionen befasst. Der Mittelwertsatz dient dazu, Punkte auf einer Funktion mit einer bestimmten Steigung zu finden. Er gilt nur unter bestimmten Voraussetzungen. Werden diese nicht erfüllt, kannst du Gegenbeispiele finden, in welchen die Aussage des Mittelwertsatzes nicht zutrifft.
Die Voraussetzungen
Betrachtet wird eine Funktion $f$ sowie der Graph dieser Funktion $G_{f}$ auf dem Intervall $[a;b]$ mit $a\neq b$. Es muss gelten:
- Die Funktion $f$ ist stetig auf dem abgeschlossenen Intervall $[a;b]$.
- Weiter muss $f$ differenzierbar auf dem offenen Intervall $(a;b)$ sein.
Die Aussage
Unter den obigen Voraussetzungen gilt dann: Es existiert mindestens ein $x_{0}\in(a;b)$ mit
$f'\left(x_{0}\right)=\dfrac{f(b)-f(a)}{b-a}$.
Der Mittelwertsatz anschaulich
Was bedeutet diese Aussage anschaulich? Schau dir das folgende Bild an:
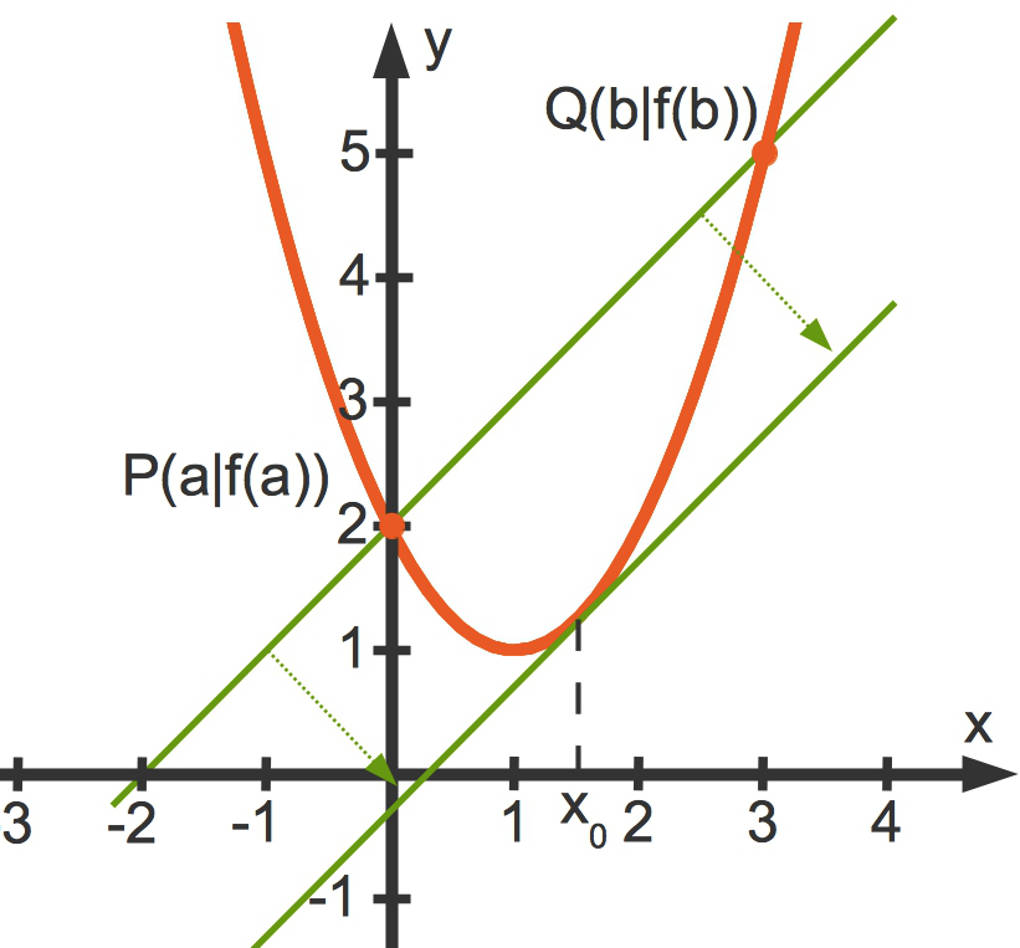
- Wenn du die Punkte $P(a|f(a))$ sowie $Q(b|f(b))$ miteinander verbindest, erhältst du eine Sekante. Dies ist eine Gerade, welche den Graphen $G_{f}$ schneidet. Die Steigung der Sekante ist $\frac{f(b)-f(a)}{b-a}$.
- Verschiebst du nun diese Sekante parallel, so berührt die parallel verschobene Gerade irgendwann $G_{f}$. Du erhältst also eine Tangente. Die Steigung der Tangente ist $f'\left(x_{0}\right)$.
- Da die Tangente durch Parallelverschiebung aus der Sekante hervorgeht, haben die beiden Geraden die gleiche Steigung.
So erhältst du die obige Aussage des Mittelwertsatzes.
Ein Beispiel für die Verletzung einer Voraussetzung:
Wenn zum Beispiel die Funktion $f$ nicht auf dem gesamten Intervall $[a;b]$ stetig ist, kannst du Folgendes beobachten. Hier siehst du einen Funktionsgraphen $G_{f}$ einer nicht stetigen Funktion $f$. Der Funktionsgraph hat eine Sprungstelle.
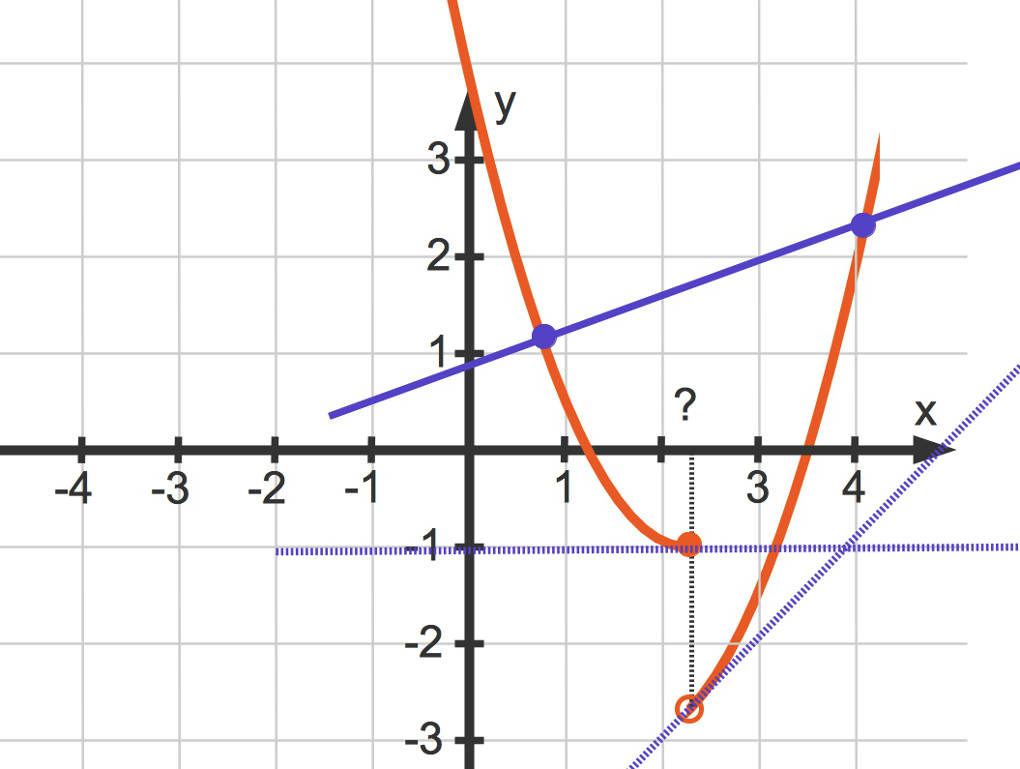
Du kannst erkennen, dass die Steigung $f'(x_0)=0$ ist. Diese ist jedoch nicht die Steigung der parallel verschobenen Sekante.
Der Satz von Rolle
Der Satz von Rolle ist ein Spezialfall des Mittelwertsatzes. Es gelten die gleichen Voraussetzungen wie beim Mittelwertsatz. Zusätzlich wird noch verlangt, dass die Funktionswerte an den Intervallrändern übereinstimmen, also $f(a)=f(b)$. Daraus folgt, dass die resultierende Sekante eine zur $x$-Achse parallele Gerade ist und damit die Steigung $0$ hat.
Die Aussage
Unter den obigen Vorraussetzungen gilt: Es existiert mindestens ein $x_{0}\in(a;b)$ mit $f'\left(x_{0}\right)=0$.
Der Satz von Rolle anschaulich
Auch hierzu schaue dir zunächst das folgende Bild an:
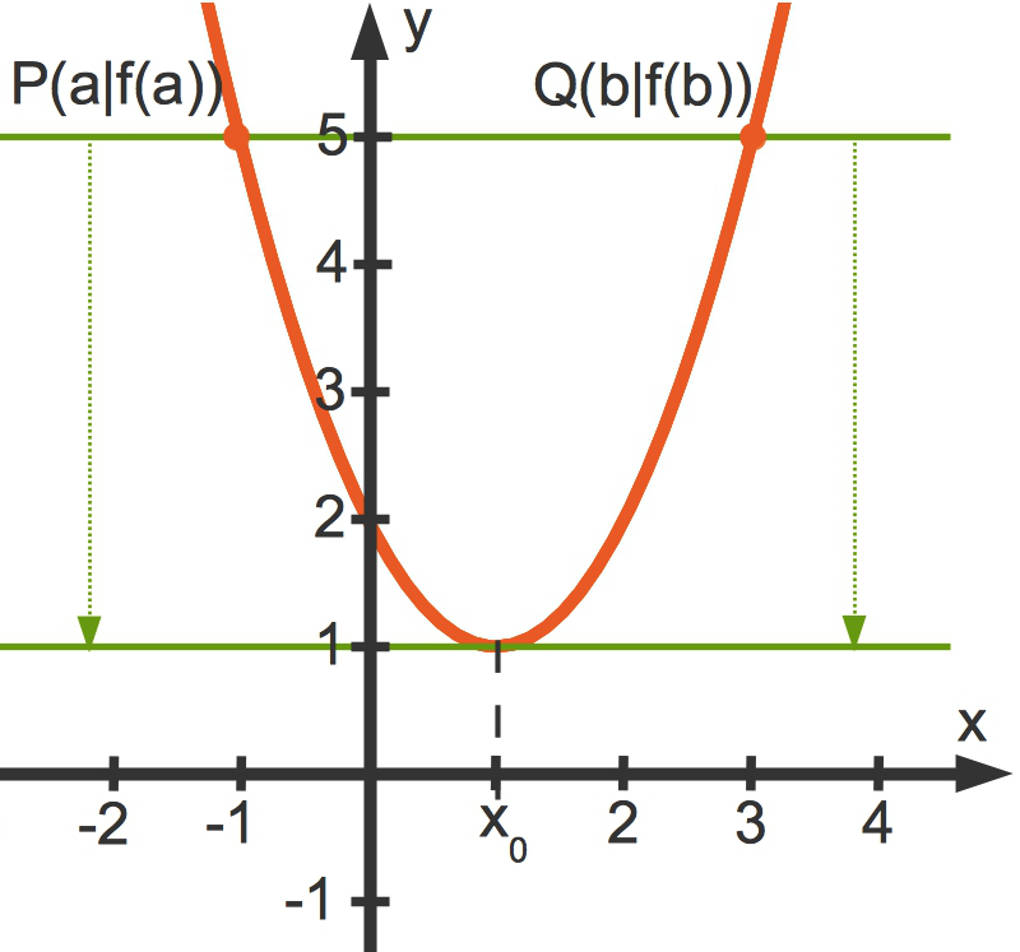
- Wie bereits festgestellt, hat die Sekante durch die Punkte $P(a|f(a))$ sowie $Q(b|f(b))$ die Steigung $0$.
- Die durch Parallelverschiebung entstandene Tangente hat dann ebenfalls die Steigung $0$.
Was ist so wichtig an dem Satz von Rolle?
Eine Stelle mit der Steigung $0$ ist eine mögliche Extremstelle. Wie du an dem obigen Bild erkennen kannst, liegt in diesem Beispiel auch tatsächlich eine Extremstelle vor. Die Aussage des Satzes von Rolle kannst du zum Beispiel im Zusammenhang mit Extremwertaufgaben verwenden.
Alle Videos zum Thema
Videos zum Thema
Mittelwertsatz (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Mittelwertsatz (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal






 Satz von Rolle
Satz von Rolle
 Mittelwertsatz der Differentialrechnung
Mittelwertsatz der Differentialrechnung









