Kathetensatz und Höhensatz
Höhe im gleichseitigen Dreieck, Diagonale eines Quadrates, Raumdiagonale eines Würfels, Raumhöhe einer Pyramide
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Die Satzgruppe des Pythagoras
Alle Sätze aus der Satzgruppe des Pythagoras gelten in rechtwinkligen Dreiecken, also Dreiecken mit einem Winkel von $90^\circ$. Diesen erkennst du an dem Punkt.
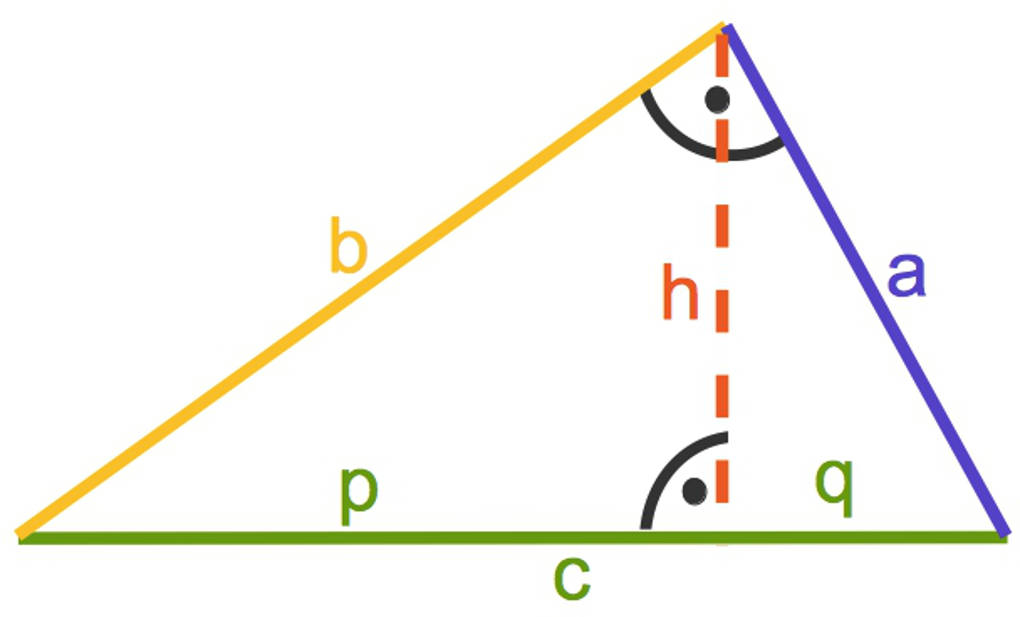
Gegenüber von dem rechten Winkel befindet sich die längste Seite des rechtwinkligen Dreiecks, die Hypotenuse $c$. Die beiden übrigen Seiten liegen an dem rechten Winkel an. Dies sind die Katheten $a$ und $b$.
Die Höhe $h$ über der Hypotenuse teilt diese in zwei Hypotenusenabschnitte $p$ und $q$. Dabei liegt $p$ an der Kathete $b$ und $q$ an der Kathete $a$ an.
Zur Satzgruppe des Pythagoras gehören:
- Der Satz des Pythagoras: Dieser besagt, dass die Summe der quadrierten Kathetenlängen gleich der quadrierten Hypotenusenlänge ist. Die bekannte mathematische Gleichung dazu lautet $a^2+b^2=c^2$. Dieser Satz ist nach Pythagoras von Samos benannt, der um 550 v. Chr. gelebt hat. Er hat angeblich als Erster den Satz mathematisch bewiesen.
- Der Kathetensatz des Euklid
- Der Höhensatz des Euklid
Euklid von Alexandria lebte im 3. Jahrhundert v. Chr. und schrieb in insgesamt 13 Büchern, „Die Elemente“, die gesamte griechische Mathematik nieder.
Der Kathetensatz des Euklid
Der Kathetensatz besagt, dass eine quadrierte Kathetenlänge gleich dem Produkt aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt ist.
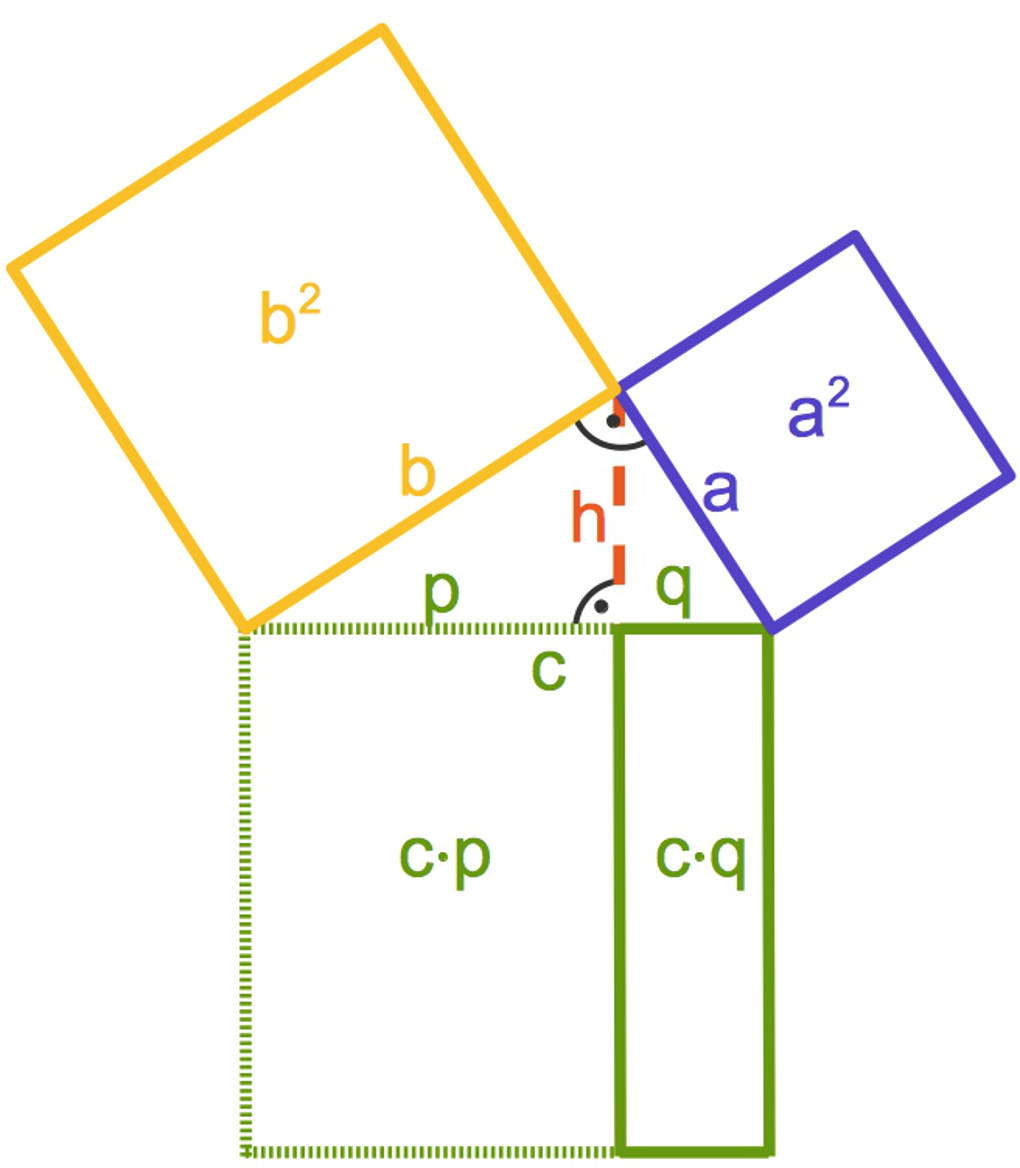
Es gilt somit für die Kathete $a$
$a^2=c\cdot q$.
Analog gilt für die Kathete $b$
$b^2=c\cdot p$.
Wie du in dem Bild erkennen kannst, ist die Summe der beiden Rechteckflächen $c\cdot p$ und $c\cdot q$ die quadrierte Hypotenuse. Es gilt
$\begin{array}{rcl} a^2+b^2&=&c\cdot q+c\cdot p\\ &=&c\cdot (q+p)\\ &=&c\cdot c\\ &=&c^2 \end{array}$
Dies ist gerade die Aussage des Satzes von Pythagoras.
Du kannst den Kathetensatz verwenden, um unbekannte Seitenlängen zu berechnen. Das fällt dann unter die Thematik Streckenlängen in Figuren berechnen.
Beispiel
Bekannt ist die Länge der Kathete $a=4$ sowie der zugehörige Hypotenusenabschnitt $q=3,2$. Berechne die Längen der Hypotenuse $c$ sowie der anderen Kathete $b$.
Mit Hilfe des Kathetensatzes erhältst du
$\begin{array}{rcll} 4^2&=&c\cdot 3,2\\ 16&=&c\cdot 3,2&\vert:3,2\\ 5&=&c \end{array}$
Da die eine Kathete $a=4$ und die Hypotenuse $c=5$ bekannt sind, kannst du die fehlende Kathete $b$ mit dem Satz des Pythagoras berechnen
$\begin{array}{rcll} 4^2+b^2&=&5^2\\ 16+b^2&=&25&\vert -16\\ b^2&=&9&\vert \sqrt{~~}\\ b&=&3 \end{array}$
Der Höhensatz des Euklid
Der Höhensatz besagt, dass die quadrierte Höhe gleich dem Produkt der Hypotenusenlängen ist.
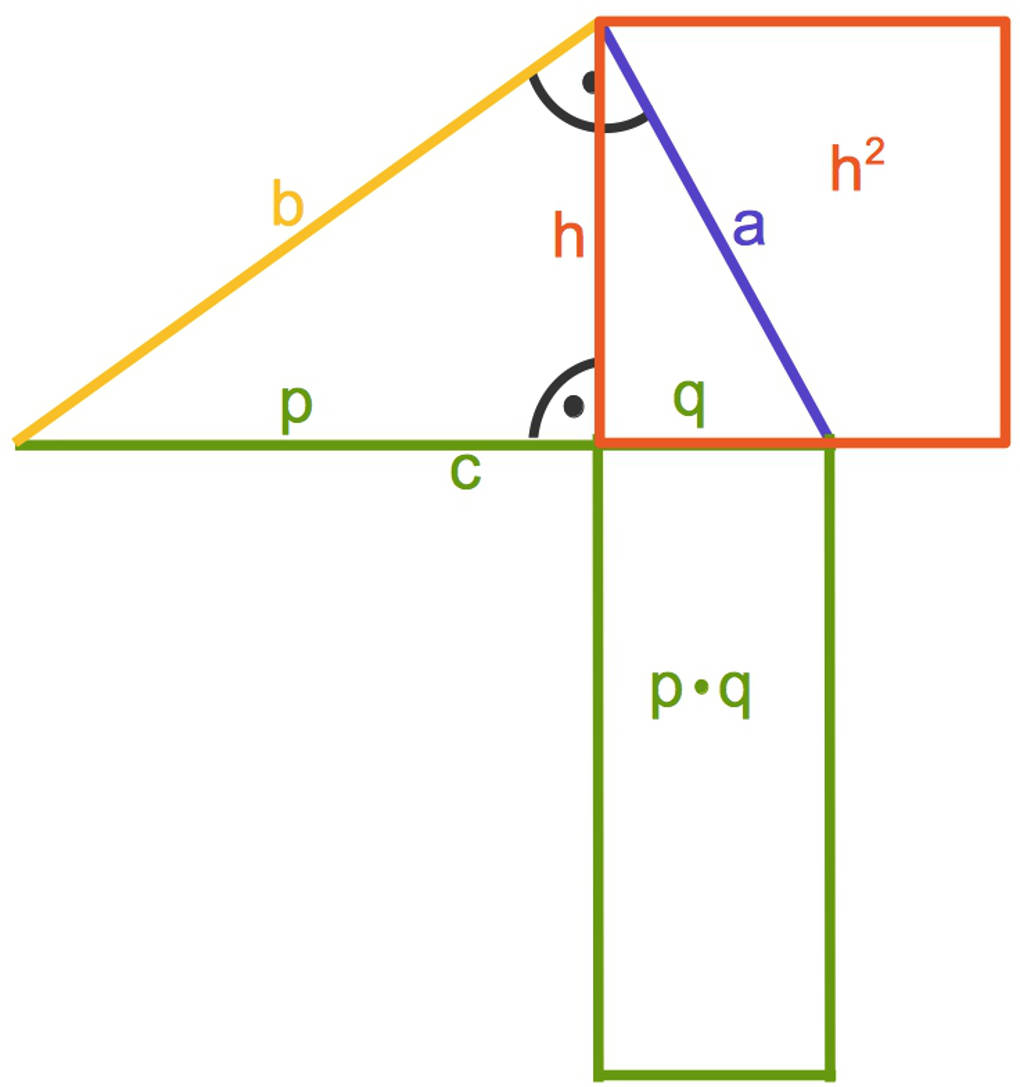
Dies bedeutet
$h^2=p\cdot q$ .
Du kannst den Höhensatz verwenden, um unbekannte Seitenlängen zu berechnen.
Beispiel: Fahnenmast
Ein senkrechter Fahnenmast ist mit zwei Spannseilen befestigt. Die beiden Spannseile treffen an der Spitze des Fahnenmastes in einem rechten Winkel aufeinander. Die Entfernungen zum Fuß des Fahnenmastes, in welcher die Spannseile am Boden befestigt sind, kannst du der Skizze entnehmen. Wie hoch ist der Fahnenmast?
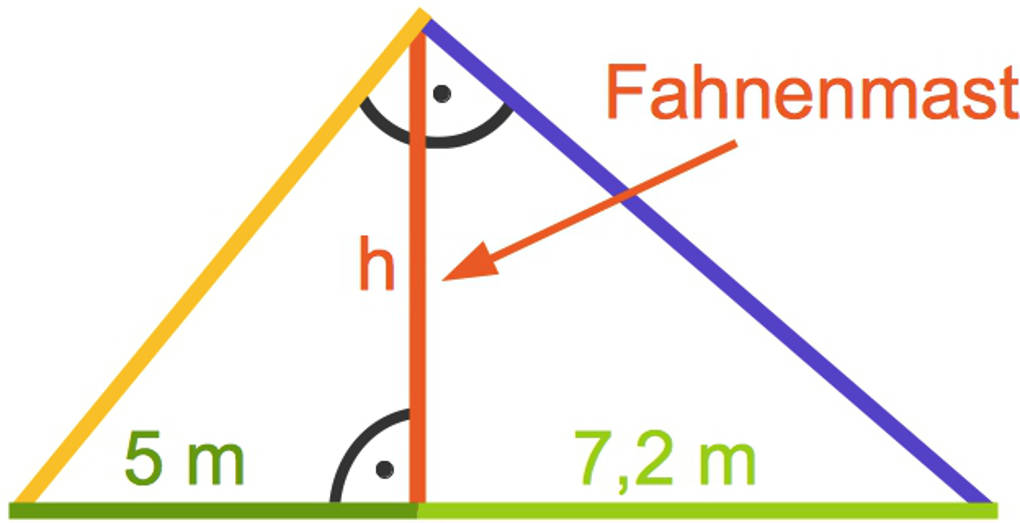
Die beiden Entfernungen sind die Hypotenusenabschnitte. Die Höhe $h$ ist unbekannt.
Es gilt
$\begin{array}{rcl} h^2&=&(5~m)\cdot (7,2~m)\\ &=&36~m^2 \end{array}$
Zuletzt wird die Wurzel gezogen. Dies führt zu der gesuchten Höhe des Fahnenmastes $h=6~m$.
Alle Videos zum Thema
Videos zum Thema
Kathetensatz und Höhensatz (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kathetensatz und Höhensatz (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal








 Kathetensatz
Kathetensatz
 Höhensatz
Höhensatz
 Streckenlängen in Figuren berechnen
Streckenlängen in Figuren berechnen
 Streckenlängen in Figuren berechnen – Übung
Streckenlängen in Figuren berechnen – Übung
 Streckenlängen in Figuren berechnen – Anwendung in Sachaufgaben
Streckenlängen in Figuren berechnen – Anwendung in Sachaufgaben









