Geradenscharen
Parameter, Ebene, Geradenbüschel, Fixpunkte
Inhaltsverzeichnis zum Thema
- Definition Geradenschar
- Scharparameter im Stützvektor
- Scharparameter im Richtungsvektor
- Scharparameter in Stütz- und Richtungsvektor
- Geradenscharen – Berechnungen
Definition Geradenschar
Eine Geradenschar besteht aus Geraden, die in der Geradengleichung einen weiteren Parameter, den sogenannten Scharparameter haben. Zu jedem Wert des Scharparameters gehört eine Gerade der Schar.
Es ist also ein Verbund von unendlich vielen, ähnlichen Geraden. Diese formale Definition klingt erstmal kompliziert. Einfacher wird es, wenn du dir die verschiedenen Fälle ansiehst. Denn der zusätzliche Parameter kann im Stützvektor, Richtungsvektor oder in beiden Vektoren vorkommen:
Scharparameter im Stützvektor
Beim folgenden Beispiel ist der Scharparameter $a$ im Stützvektor der Parameterdarstellung der Geraden $g_{a}$. Sowohl für $a$ als auch für $t$ kannst du eine beliebige reelle Zahl einsetzen, es gilt also: $a,t\in\mathbb{R}$. Die Geradengleichung lautet:
$g_{a}:\vec x=\begin{pmatrix} 1-a \\ 2a\\ 3+a \end{pmatrix}+t\cdot \begin{pmatrix} 2 \\ 1\\ -1 \end{pmatrix}$
Der Stützvektor hängt also von $a$ ab, er ist nicht fix. In unserem Beispiel hängen alle drei Koordinaten von $a$ ab. Es handelt sich aber auch um eine Geradenschar, wenn z.B. nur eine Koordinate von einem Scharparameter abhängt.
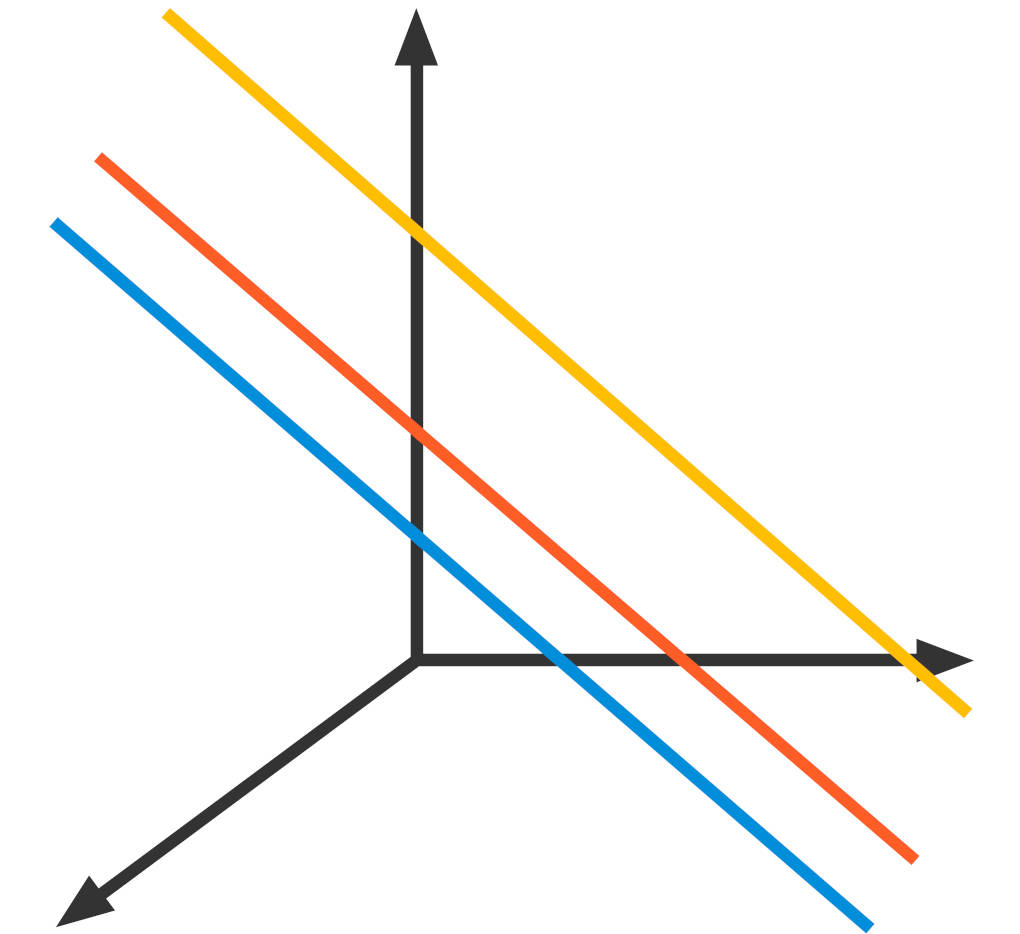
Der Richtungsvektor ist allerdings fixiert. Das bedeutet, dass alle Geraden der Geradenschar die gleiche Richtung im Raum haben. Sie sind also parallel zueinander. Man nennt eine solche Geradenschar auch Parallelenschar.
Scharparameter im Richtungsvektor
Im nächsten Beispiel ist der Scharparameter im Richtungsvektor der Parameterdarstellung der Geraden $h_{a}$. Auch hier soll wieder gelten, dass für beide Parameter eine beliebige reelle Zahl eingesetzt werden kann:
$h_{a}:\vec x=\begin{pmatrix} 1\\ 2\\ 3 \end{pmatrix}+t\cdot \begin{pmatrix} 2a\\ -3+a\\ a \end{pmatrix}$
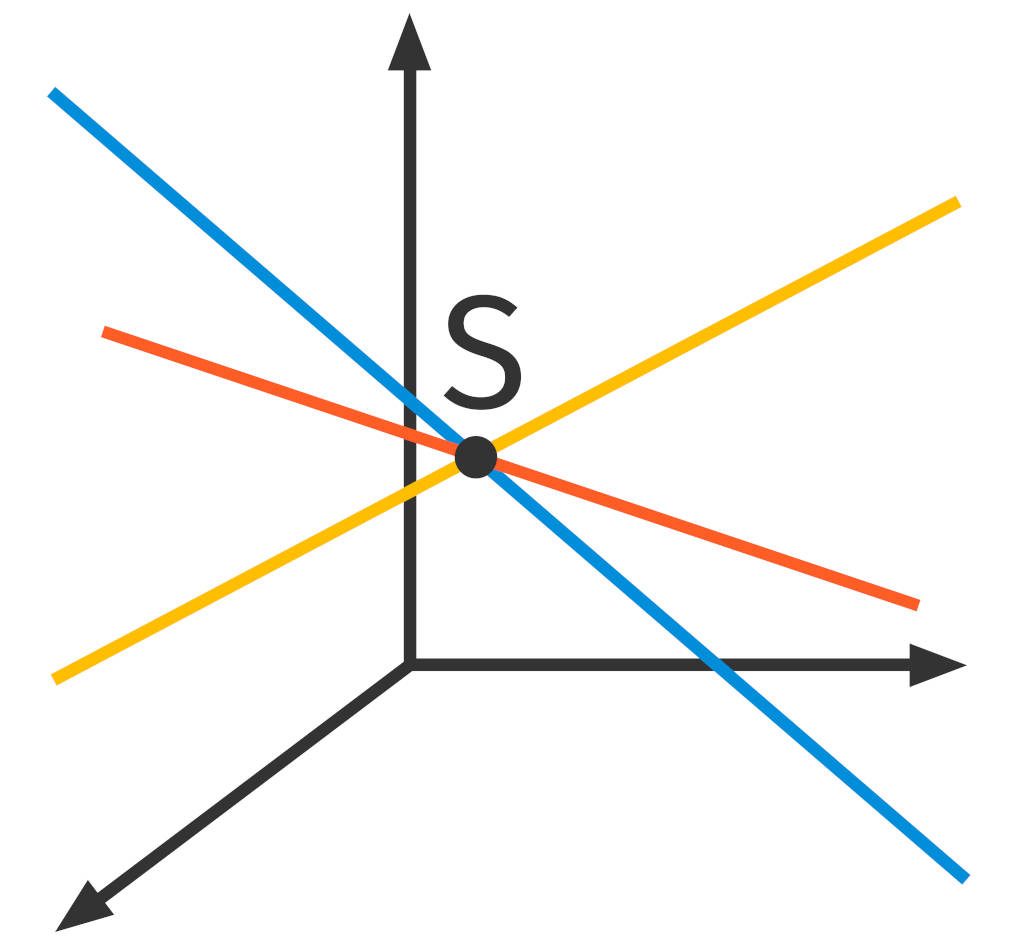
Der Stützvektor ist bei allen Geraden der Geradenschar gleich. Das bedeutet, dass diese durch den gemeinsamen Fixpunkt $S(1|2|3)$ verlaufen. Es bildet sich ein sogenanntes Geradenbüschel. Nur der Richtungsvektor hängt vom Parameter $a$ ab. Somit hat jede Gerade der Schar eine andere Steigung bzw. Richtung im Raum.
Scharparameter in Stütz- und Richtungsvektor
Was ist aber nun, wenn der Scharparameter $a$ sowohl im Stütz- als auch im Richtungsvektor vorkommt? Sieh dir dazu folgendes Beispiel an:
$h_{a}:\vec x=\begin{pmatrix} 1-a\\ 2a\\ 3+a \end{pmatrix}+t\cdot \begin{pmatrix} 5a\\ -3a\\ a \end{pmatrix}$
Diese Parametergleichung können wir aber umformen:
$\vec x=\begin{pmatrix} 1-a+5at\\ 2a-3at\\ 3+a+at \end{pmatrix}=\begin{pmatrix} 1+a(-1+5t)\\ a(2-3t)\\ 3+a(1+t) \end{pmatrix}=\begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}+a\cdot \begin{pmatrix} -1+5t\\ 2-3t\\ 1+t \end{pmatrix}$
Nun ist $t$ der Scharparameter. Hättest du das erwartet? Wenn du willst, kannst du auch $t$ und $a$ gegeneinander austauschen. Denn auf die Bezeichnungen kommt es nicht an. Tatsächlich kannst du also manche Geradenscharen so umformen, dass der Scharparameter nur noch im Stütz- oder Richtungsvektor vorkommt.
Ist dies nicht möglich, so hängen beide Vektoren vom Scharparameter ab. Solch eine Schar kannst du nicht mehr geometrisch deuten. Die Geraden verlaufen nicht durch einen Fixpunkt und die Richtung einer jeder Geraden ist anders.
Geradenscharen – Berechnungen
Keine Angst vor Geradenscharen! Denn egal, ob du eine einzelne Gerade gegeben hast oder eine ganze Geradenschar: Die grundsätzlichen Vorgehensweisen bei vielen Berechnungen bleiben gleich!
Die Ergebnisse sind allerdings oft nicht konkret, sondern hängen vom Scharparameter ab. Zum Beispiel bei der Berechnung der Schnittpunkte mit den Koordinatenachsen.
Manchmal ist aber auch gefragt, welchen konkreten Wert der Scharparameter annehmen muss, damit ein bestimmter Sachverhalt erfüllt ist. Zum Beispiel, welche Gerade der Schar durch einen bestimmten Punkt verläuft.
Alle Videos zum Thema
Videos zum Thema
Geradenscharen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Geradenscharen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter





 Geradenscharen
Geradenscharen
 Geradenscharen – Berechnungen
Geradenscharen – Berechnungen









