Kreisgleichungen in der Ebene und gegenseitige Lage Punkt-Kreis
Vektorgleichung, Koordinatengleichung, 3 Punkte, Punktprobe, relative Lage
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Grundlagen des Kreises
- Kreisgleichungen
- Kreisgleichung aufstellen mit drei Punkten
- Gegenseitige Lage Punkt-Kreis
Grundlagen des Kreises
Sieh dir zunächst die Definition des Kreises in der Ebene als Punktemenge an: Zur Kreislinie gehören jene Punkte, die von einem Mittelpunkt $M$ genau den Abstand $r$ haben.
Stell dir nun vor, du hast einen beliebigen Kreis gegeben. Dieser ist in einem $x$-$y$-Koordinatensystem eingezeichnet. Du möchtest nun z.B. von einem gegebenen Punkt $Q$ wissen, ob dieser auf der Kreislinie liegt. Damit es genau wird, musst du das rechnerisch zeigen.
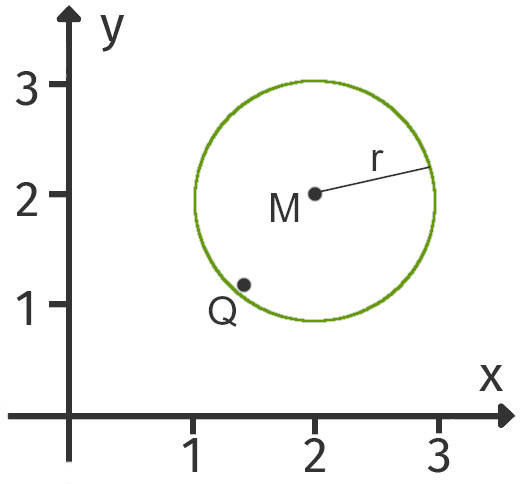
Allein mit der obigen Definition wird das schwierig. Aber was würdest du sagen, wenn du einen konkreten Term für den Kreis hättest? Tatsächlich kannst du jeden Kreis mithilfe der Koordinaten $x$ und $y$ oder mithilfe von Vektoren darstellen! Diese Darstellungen werden Kreisgleichungen genannt.
Kreisgleichungen
Im Folgenden siehst du zunächst, wie du einen beliebigen Kreis mithilfe von Vektoren darstellen kannst. Damit leitest du die allgemeine Vektorgleichung her:
Vektorgleichung
Gegeben sei ein Kreis mit dem Mittelpunkt $M(m_1|m_2)$ und dem Radius $r$. Ebenso ist ein Punkt $P(x|y)$ auf der Kreislinie gegeben. Den Ursprung bezeichnest du mit $O(0|0)$.
Subtrahiere den Ortsvektor des Punktes $P$ von dem des Punktes $M$. Die Länge dieses Vektors, also der Betrag, ist genau der Radius $r$. Deshalb kannst du folgende allgemeine Vektorgleichung festhalten:
$\begin{array}{rcl} |\vec{OP}-\vec{OM}| & = & r \\ \left|\begin{pmatrix}x-m_1\\y-m_2\end{pmatrix}\right|&=& r \\ \begin{pmatrix}x-m_1\\y-m_2\end{pmatrix}^2 &=& r^2 \\ \end{array}$
Koordinatengleichung
Mit der allgemeinen Vektorgleichung des Kreises kannst du ganz einfach die allgemeine Koordinatengleichung herleiten:
$\begin{array}{rcl} \begin{pmatrix}x-m_1\\y-m_2\end{pmatrix}^2 &=& r^2 \\ \begin{pmatrix}x-m_1\\y-m_2\end{pmatrix}\cdot \begin{pmatrix}x-m_1\\y-m_2\end{pmatrix} &=& r^2 \\ (x-m_1)^2 + (y-m_2)^2 &=& r^2 \\ \end{array}$
Die Kreisgleichung kann auch nach der Veränderlichen $y$ aufgelöst werden:
$\begin{array}{llll}(x-m_1)^2 + (y-m_2)^2 & = & r^2 & |-(x-m_1)^2\\ (y-m_2)^2 & = & r^2 - (x-m_1)^2 & |\sqrt{\quad}\\ y-m_2 & = & \pm \sqrt{ r^2 -(x-m_1)^2} & |+m_2\\ y & = & m_2 \pm \sqrt{ r^2 -(x-m_1)^2} &\\ \end{array}$
Jetzt siehst du auch, dass es sich bei der Kreisgleichung nicht um eine Funktion handelt. Denn bei Funktionen darf es zu einem $x$ höchstens einen $y$-Wert geben.
Sofern du also den Mittelpunkt und den Radius kennst, kannst du ganz schnell die Gleichung für den Kreis aufstellen. Doch was ist, wenn dir diese Größen nicht bekannt sind, weil du z.B. nur drei Punkte auf dem Kreis kennst?
Kreisgleichung aufstellen mit drei Punkten
Liegen drei verschiedene Punkte nicht auf einer gemeinsamen Geraden, bestimmen sie einen Kreis. Die Kreisgleichung kann dann eindeutig berechnet werden.
Du hast nun die drei Punkte $A(1|2)$, $B(2|1)$ und $C(2|3)$ gegeben. Diese bilden im $x$-$y$-Koordinatensystem ein Dreieck. Der gesuchte Kreis ist also der Umkreis des Dreiecks. Den Umkreismittelpunkt findest du heraus, indem du den Schnittpunkt von zwei Mittelsenkrechten berechnest.
Dafür benötigst du natürlich zunächst die Gleichungen zweier Mittelsenkrechten. Diese stellst du mit Vektoren auf. Sieh dir dafür folgende Skizze an:
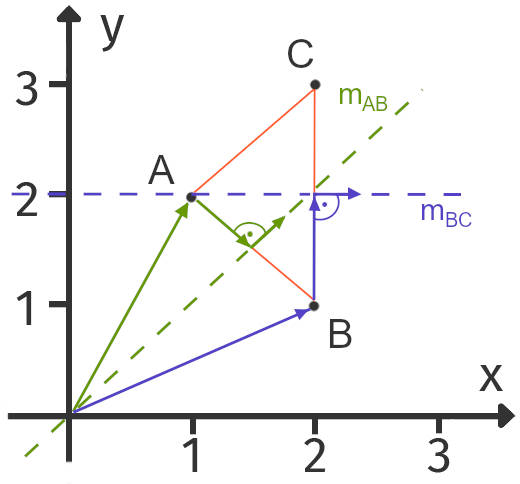
Für die Geradengleichung oder auch Parametergleichung der Mittelsenkrechten $m_{AB}$ von der Strecke $AB$ brauchst du folgenden Vektor:
$\vec{AB} = \vec {OB} - \vec {OA} = \begin{pmatrix}2-1\\1-2\end{pmatrix}=\begin{pmatrix}1\\-1\end{pmatrix}$
Zu diesem Vektor suchst du einen senkrechten Vektor $\vec{n_1}$. Dafür muss ihr Skalarprodukt null sein:
$\begin{array}{rcl} \vec{n_1}\cdot\vec{AB} &=& 0 \\ \begin{pmatrix}n_x\\n_y\end{pmatrix}\cdot\begin{pmatrix}1\\-1\end{pmatrix} &=& 0 \\ n_x-n_y &=& 0\\ n_x &=& n_y\\ \end{array}$
Die $x$-Koordinate ist also gleich der $y$-Koordinate des Vektors. Du kannst also z.B. folgenden Vektor wählen:
$\vec{n_1}=\begin{pmatrix}1\\1\end{pmatrix}$
Damit kannst du die Parametergleichung von $m_{AB}$ angeben. Der griechische Buchstabe $\lambda$ steht dabei für eine beliebige Zahl aus $\mathbb{R}$.
$\begin{array}{lll} \vec{OA} + \frac{1}{2}\cdot\vec{AB} + \lambda \cdot \vec{n_1} &=& \begin{pmatrix} 1\\ 2\end{pmatrix} + \frac{1}{2}\cdot\begin{pmatrix} 1 \\ -1\end{pmatrix} + \lambda \cdot \begin{pmatrix} 1\\ 1\end{pmatrix} \\ &=& \begin{pmatrix} 1,5 \\ 1,5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1\\ 1\end{pmatrix} \\ &=& \lambda \cdot \begin{pmatrix} 1\\ 1\end{pmatrix} \end{array}$
Der Stützvektor hat die gleiche Richtung wie der Richtungsvektor, deshalb kann man diesen weglassen. Für die Parametergleichung der Mittelsenkrechten der Strecke $\overline{BC}$ gehen wir analog vor. Der Vektor $\vec{n_2}$ ist dabei so gewählt, dass er auf der Strecke $\overline{BC}$ senkrecht steht.
$\begin{array}{lll} \vec{OB} + \frac{1}{2}\cdot\vec{BC} + \mu \cdot \vec{n_2} &=& \begin{pmatrix} 2\\ 1\end{pmatrix} + \frac{1}{2}\cdot\begin{pmatrix} 0\\ 2\end{pmatrix} + \mu \cdot \begin{pmatrix} 1\\ 0\end{pmatrix} \\ &=& \begin{pmatrix} 2\\ 2\end{pmatrix} + \mu \cdot \begin{pmatrix} 1\\ 0\end{pmatrix} \end{array}$
Um den Schnittpunkt und damit den Umkreismittelpunkt zu bestimmen, setzt du die Parameterdarstellungen der Mittelsenkrechten gleich:
$\lambda \cdot \begin{pmatrix} 1\\ 1\end{pmatrix} =\begin{pmatrix} 2\\ 2\end{pmatrix} + \mu \cdot \begin{pmatrix} 1\\ 0\end{pmatrix} $
$\begin{array}{rcl} \lambda &=& 2+ \mu\\ \lambda &=& 2\\ \end{array}$
Du erhältst für $\lambda = 2$ und für $\mu = 0$. Den Schnittpunkt erhältst du durch Einsetzen in die Parameterdarstellung einer Mittelsenkrechten deiner Wahl. Zum Beispiel in $m_{AB}$:
$2\cdot \begin{pmatrix} 1\\ 1\end{pmatrix} =\begin{pmatrix} 2\\ 2\end{pmatrix} $
Nun kannst du auch den Radius $r$ des Umkreises bestimmen. Dafür berechnest du den Abstand eines Punktes vom Mittelpunkt:
$\begin{array}{rcl} |\vec{OA}-\vec{OM}|&=& \left|\begin{pmatrix} 1\\ 2\end{pmatrix}-\begin{pmatrix} 2\\ 2\end{pmatrix} \right | \\ &=& \left |\begin{pmatrix} -1\\ 0\end{pmatrix}\right | \\ &=& \sqrt{(-1)^2 + 0^2} &=& 1 \end{array}$
Der Radius ist also eins. Damit lautet die Kreisgleichung in Koordinatenform für das Beispiel:
$(x-2)^2 + (y-2)^2 = 1^2 $
Alternativ kannst du die Kreisgleichung bestimmen, indem du drei Gleichungen aufstellst. Dafür setzt du in die allgemeine Koordinatengleichung des Kreises die Punkte $A(1|2)$, $B(2|1)$ und $C(2|3)$ ein:
$ \begin{array}{llll} A: & (1-m_1)^2 + (2-m_2)^2 & = & r^2 \\ B: & (2-m_1)^2 + (1-m_2)^2 & = & r^2 \\ C: & (2-m_1)^2 + (3-m_2)^2 & = & r^2 \\ \end{array} $
Dieses Gleichungssystem kannst du z.B. durch das Gauß-Verfahren lösen.
Gegenseitige Lage Punkt-Kreis
Sieh dir den Punkt $Q(1,5|1,2)$ an. Welche gegenseitige Lage haben Punkt und Kreis, wenn die Kreisgleichung wie folgt lautet:
$(x-2)^2+(y-2)^2 = 1^2$
Berechne zunächst den Abstand $d(Q,M)$ von $Q$ zum Mittelpunkt, welcher immer positiv definiert ist:
$\begin{array}{lll} (1,5-2)^2 + (1,2-2)^2 & = & d(Q,M)^2\\ (-0,5)^2 + (-0,8)^2 & = & d(Q,M)^2 \\ 0,25 + 0,64 & = & d(Q,M)^2\\ \sqrt{0,89} &=& d(Q,M)\\ \end{array}$
Der Punkt $Q$ liegt also nicht auf der Kreislinie, denn sonst wäre sein Abstand zum Mittelpunkt genau der Radius ($r=1$). Der Abstand ist kleiner als eins, daher liegt $Q$ im Kreisinneren. Den Abstand von $Q$ zur Kreislinie kannst du ebenfalls berechnen:
$\begin{array}{lll} \left|r-\sqrt{0,89}\right| & = & \left|1-\sqrt{0,89}\right| \\ & \approx & 0,06 \end{array}$
Alle Videos zum Thema
Videos zum Thema
Kreisgleichungen in der Ebene und gegenseitige Lage Punkt-Kreis (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kreisgleichungen in der Ebene und gegenseitige Lage Punkt-Kreis (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Kreisgleichungen in der Ebene
Kreisgleichungen in der Ebene
 Kreisgleichungen mit drei Punkten bestimmen
Kreisgleichungen mit drei Punkten bestimmen
 Gegenseitige Lage Punkt-Kreis in der Ebene
Gegenseitige Lage Punkt-Kreis in der Ebene












