Mengenlehre
Die Mengenlehre beschäftigt sich mit Mengen. Man kann aus einer oder mehreren Mengen weitere Mengen durch Mengenoperationen erzeugen oder sie miteinander durch Mengenrelationen vergleichen.
Beliebteste Videos und Lerntexte
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine Menge?
- Die Menge der natürlichen Zahlen
- Die Mengenschreibweise
- Die Kardinalität einer Menge
- Das Elementzeichen
- Wie können Mengen dargestellt werden?
- Welche Beziehungen können zwischen Mengen gelten?
- Mengenoperationen
Was ist eine Menge?
Wir schauen uns zunächst einmal die Definition von Georg Ferdinand Ludwig Philipp Cantor (1845-1918) an. Georg Cantor war ein deutscher Mathematiker und gilt als der Begründer der Mengenlehre. Er sagt:
„Unter einer Menge verstehen wir jede Zusammenfassung $M$ von bestimmten wohlunterschiedenen Objekten ($e$) unserer Anschauung oder unseres Denkens (welche die Elemente von $M$ genannt werden) zu einem Ganzen.“
Das hört sich ziemlich kompliziert an. Schauen wir uns also gleich einmal ein paar Beispiele für Mengen an. Wir werden sehen, das ist gar nicht so kompliziert.
Die Menge der natürlichen Zahlen
Du kennst sicher schon die Menge der natürlichen Zahlen $\mathbb{N}=\{0;1;2;3;4;...\}$. Hinter der $4$ folgen noch viele weitere Zahlen. Dies wird durch drei Punkte angedeutet.
Jede einzelne Zahl, also $0$, $1$, $2$, $3$, $4$ und so weiter, wird als Element der Menge $\mathbb{N}$ bezeichnet.
Die Mengenschreibweise
Du schreibst die Elemente einer Menge immer in geschwungenen Klammern:
- Links steht die öffnende Klammer „$\{$“ und
- rechts steht die schließende Klammer „$\}$“.
Beispiele:
- $M_1=\{$Kopf, Zahl$\}$
- $M_2=\{2;3;5;7;11;...\}$, die Menge der Primzahlen
- $M_3=\{\}$: Da ist ja gar kein Element in der Menge. Wir nennen dies die „leere“ Menge. Die kannst du auch so schreiben: $M=\emptyset$.
- $M_4=\{a;b;c;d\}$
Die Kardinalität einer Menge
Bei einigen Mengen kannst du zählen, wie viele Elemente sich in dieser Menge befinden. Die Anzahl der Elemente einer Menge wird als Kardinalität card$(M)$ oder auch Mächtigkeit der Menge $M$ bezeichnet.
- card$(M_1)=2$
- In $M_2$ befinden sich unendlich viele Elemente.
- card$(M_3)=0$
- card$(M_4)=4$
Das Elementzeichen
Die Schreibweise dafür, dass ein Element $e$ in einer Menge $M$ liegt, sieht so aus:
$e\in M$.
Wir sagen „$e$ ist ein Element von $M$.“ oder „$e$ liegt in der Menge $M$.“ $\in$ ist das Elementzeichen.
Wenn ein Element nicht in einer Menge liegt, wird das Elementzeichen durchgestrichen. $e\not \in M$ bedeutet also, dass $e$ nicht in $M$ liegt.
Zusammenfassend können wir feststellen, dass eine Menge eine Gesamtheit von Elementen ist.
Wie können Mengen dargestellt werden?
Die Aufzählung aller Elemente
Eine Menge kann durch Aufzählung all ihrer Elemente dargestellt werden. Dies ist natürlich nur dann möglich, wenn dies nicht zu viele oder sogar unendlich viele Elemente sind:
$M=\{1;2;3;4\}$.
Wenn sich viel mehr Elemente in der Menge befinden, wird dies wenn möglich mit drei Punkten abgekürzt. Die natürlichen Zahlen von $1$ bis $100$ lassen sich mit der sogenannten elliptischen Schreibweise aufschreiben:
$M=\{1;2;3;...;98;99;100\}$.
Es wäre viel zu aufwändig, alle Elemente aufzuschreiben. Manchmal ist auch dies nicht möglich.
Die Beschreibung der Elemente
Auch hier schauen wir uns wieder einen Zahlenbereich an, nämlich den der rationalen Zahlen oder auch Bruchzahlen:
$\mathbb{Q}=\left\{\frac ab;~a\in\mathbb{Z};~b\in \mathbb{N};~b\neq 0\right\}$.
Mit dieser mathematischen Formulierung werden alle rationalen Zahlen beschrieben.
Du könntest auch eine andere Eigenschaft beschreiben:
$M=\{x~|~x$ ist ein Wochentag$\}$.
Dies kannst du wie folgt lesen: „$M$ ist die Menge aller $x$, für die gilt, dass $x$ ein Wochentag ist.“ Diese Menge kannst du auch in aufzählender Schreibweise darstellen:
$M=\{$Montag, Dienstag, Mittwoch, Donnerstag, Freitag, Samstag, Sonntag$\}$.
Welche Beziehungen können zwischen Mengen gelten?
Die Teilmengenbeziehung
Eine Menge $B$ kann komplett in einer anderen Menge $A$ liegen.
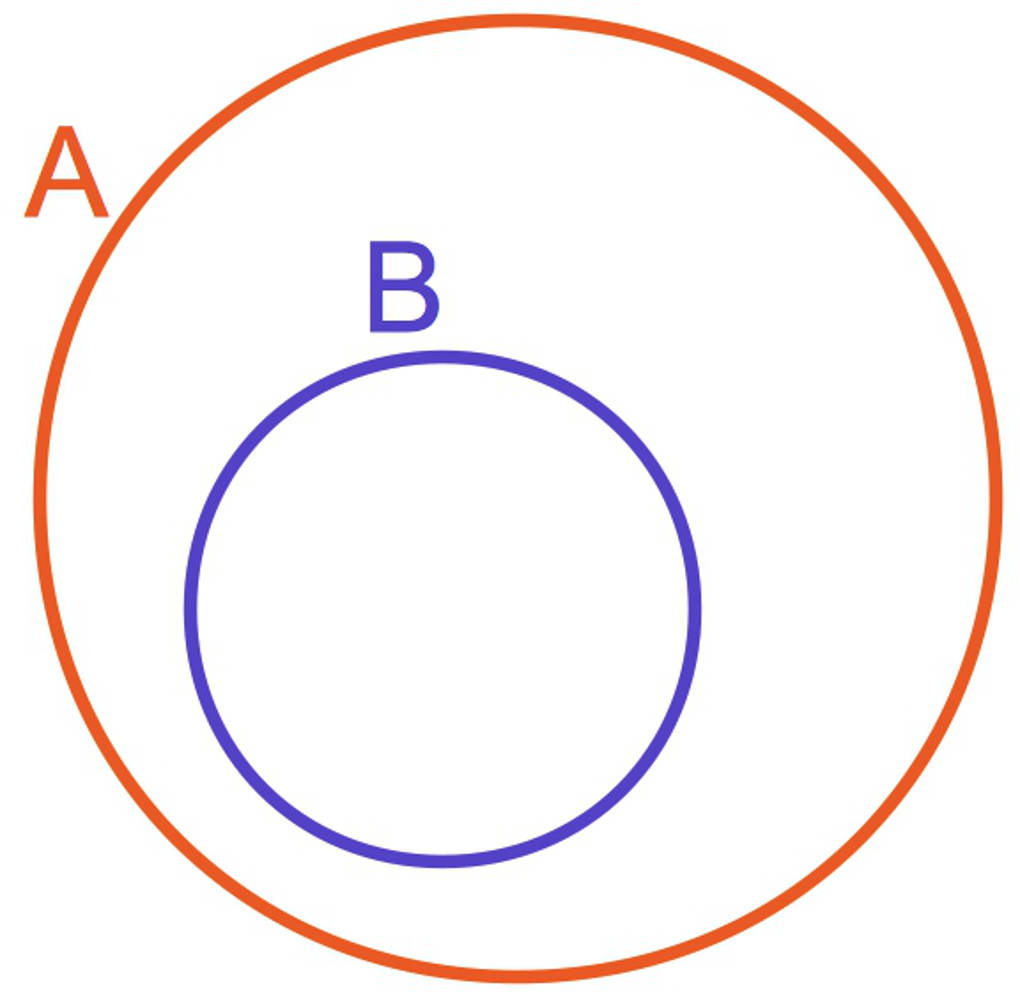
Das bedeutet, dass jedes Element, welches in $B$ liegt, auch gleichzeitig in $A$ liegt. Aus $e\in B~$ folgt, dass $~e\in A$.
Die Schreibweise für die Teilmengenbeziehung sieht so aus: $B\subset A$. Wir sagen „$B$ ist eine Teilmenge von $A$.“
Beispiel:
- $A=\{1;2;3;4;5;6\}$, die natürlichen Zahlen von $1$ bis $6$, und
- $B=\{2;4;6\}$, die ganzen Zahlen bis zur Zahl $6$.
Jede Zahl, die in $B$ liegt, liegt auch in $A$. Mathematisch schreiben wir also $B\subset A$.
Übrigens gibt es auch das Zeichen „$\subseteq$“. Es bedeutet, dass die eine Menge eine Teilmenge der anderen ist, dass die Mengen aber theoretisch auch identisch sein können.
Schauen wir uns eine Darstellung der Zahlenbereiche an. Welche Zahlenbereiche kennst du schon?
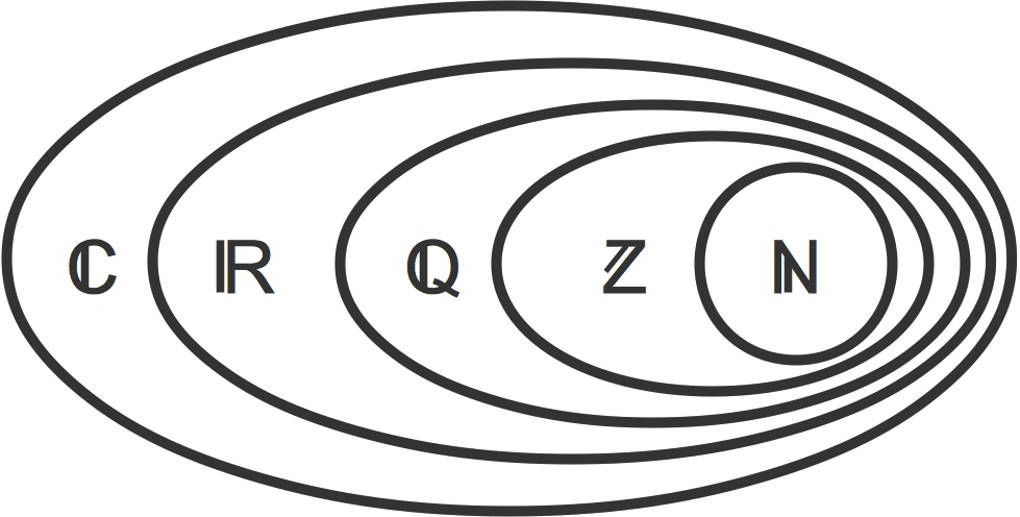
Auch hier gilt die Teilmengenbeziehung: Die Menge der natürlichen Zahlen ist eine Teilmenge der ganzen Zahlen. Die ganzen Zahlen sind wiederum eine Teilmenge der rationalen Zahlen. Die Menge der rationalen Zahlen ist eine Teilmenge der reellen Zahlen. Es gibt noch einen weiteren Zahlenbereich, den der komplexen Zahlen. Die Menge der reellen Zahlen ist eine Teilmenge der komplexen Zahlen.
Folgende Eigenschaften gelten in diesen Zahlenbereichen:
- Jede natürliche Zahl ist auch eine ganze Zahl.
- Jede ganze Zahl ist auch eine rationale Zahl.
- Jede rationale Zahl ist auch eine reelle Zahl.
- Jede reelle Zahl ist auch eine komplexe Zahl.
Umgekehrt gilt dies aber nicht. Nicht jede ganze Zahl ist auch eine natürliche Zahl (zum Beispiel $-2$).
$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$
Die Mengengleichheit
Zwei Mengen heißen gleich, wenn all ihre Elemente übereinstimmen: $A=B$.
Beispiel:
- $A=\{1;2;3;4;5;6\}$
- $B=\{x\in\mathbb{N}~|~x\le 6\}$
$B$ beschreibt ebenfalls die natürlichen Zahlen von $1$ bis $6$, nur dass die Menge hier in beschreibender Weise angegeben ist.
Zwei Mengen sind verschieden
Zwei Mengen können auch komplett verschieden sein. Das bedeutet, dass es keine Elemente gibt, die sowohl in der einen Menge als auch in der anderen liegen.
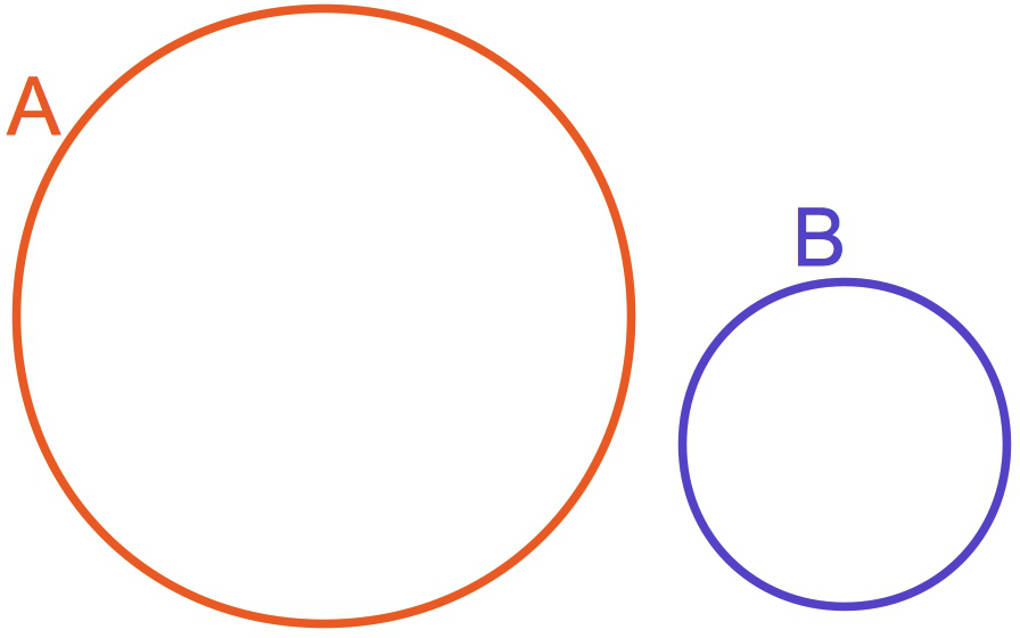
Solche Mengen werden auch elementefremd oder durchschnittsfremd genannt. Dafür gibt es einen weiteren Begriff. Wir sagen: „Diese beiden Mengen sind disjunkt.“
Beispiel:
- $A=\{1;2;3;4;5;6\}$
- $B=\{7;8;9;10;11;12\}$
In $A$ befinden sich die natürlichen Zahlen $1$ bis $6$ und in $B$ die natürlichen Zahlen $7$ bis $12$. Offensichtlich kommen keine Elemente doppelt vor. $A$ und $B$ sind also disjunkt.
Mengenoperationen
Mengen können auch miteinander verknüpft werden. Im Folgenden lernst du verschiedene Mengenoperationen kennen.
Der Schnitt zweier Mengen
Der Schnitt zweier Mengen $A$ und $B$ ist wieder eine Menge. In dieser Menge befinden sich alle Elemente, die sich in der Menge $A$ und in der Menge $B$ befinden. Der mengentheoretische Schnitt entspricht dem logischen „und“:
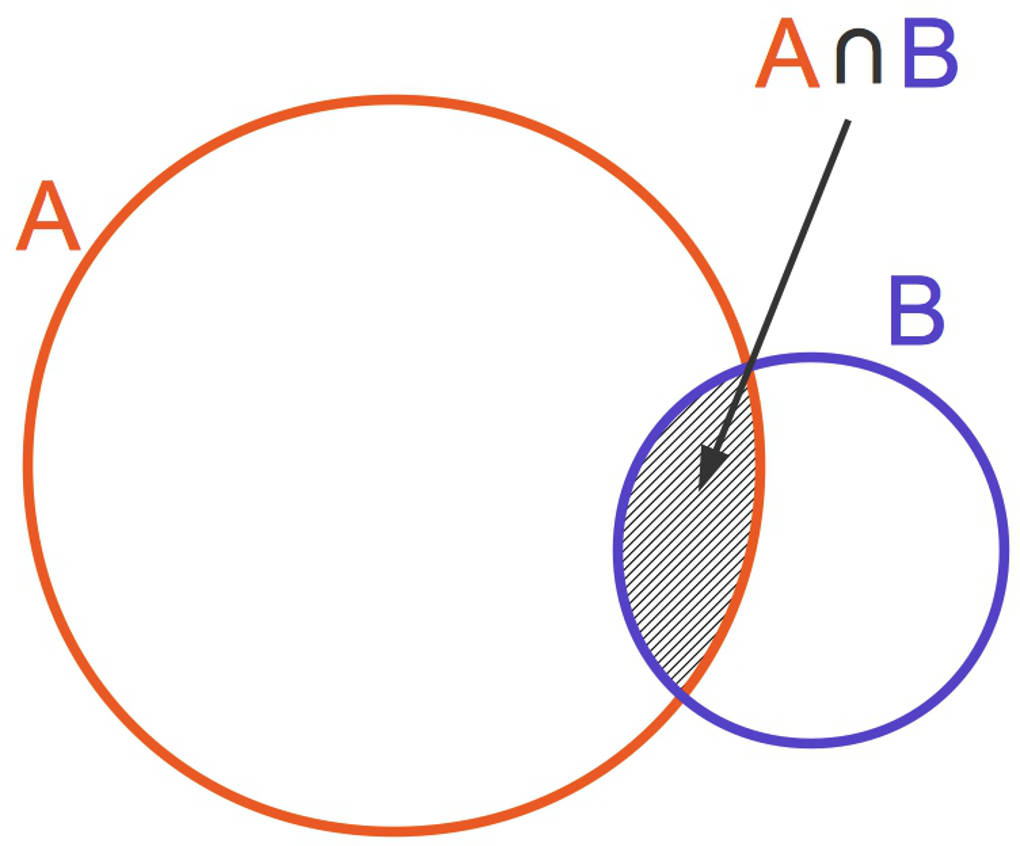
$A\cap B=\{x~|~x\in A~\text{und}~x\in B\}$.
Beispiel:
- $A=\{1;2;3;4;5;6\}$
- $B=\{4;5;6;7;8;9;10\}$
Dann ist $A\cap B=\{4;5;6\}$.
Die Vereinigung zweier Mengen
Die Vereinigung zweier Mengen $A$ und $B$ ist auch wieder eine Menge. In dieser Menge befinden sich alle Elemente, die sich in der Menge $A$ oder in der Menge $B$ befinden. Die mengentheoretische Vereinigung entspricht demzufolge logischen „oder“:
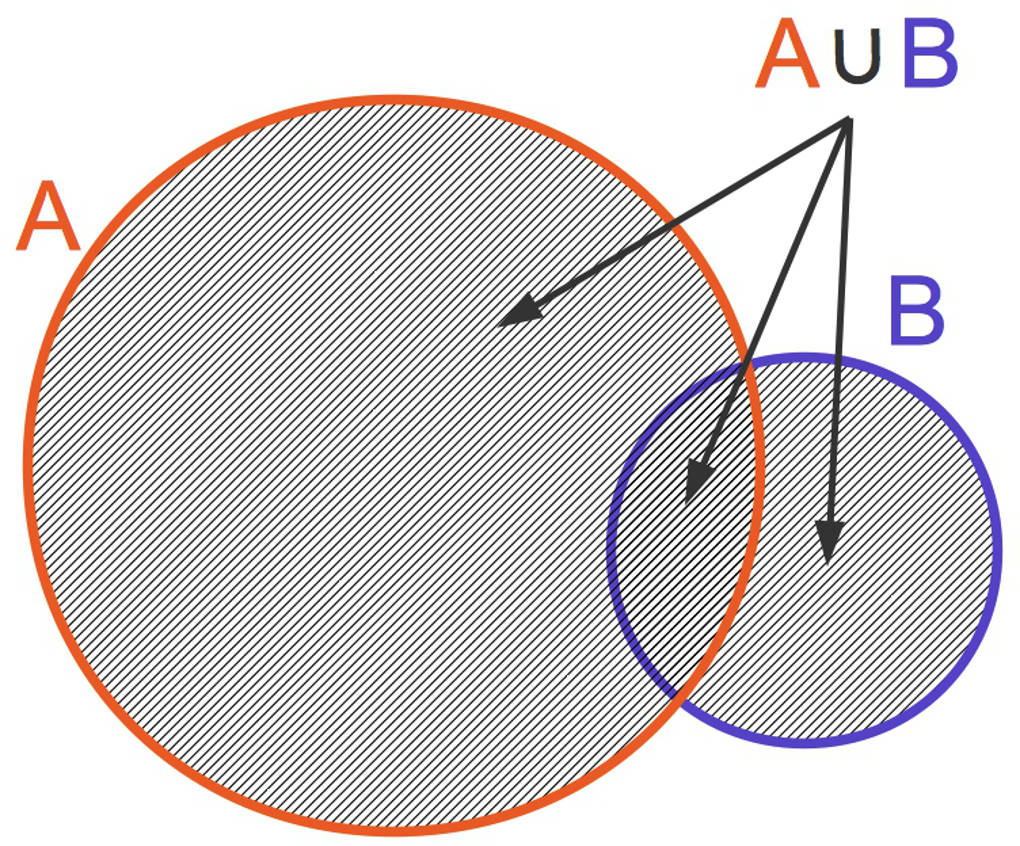
$A\cup B=\{x~|~x\in A~\text{oder}~x\in B\}$.
Beispiel:
- $A=\{1;2;3;4;5;6\}$
- $B=\{4;5;6;7;8;9;10\}$
Dann ist $A\cup B=\{1;2;3;4;5;6;7;8;9;10\}$.
Die Mengendifferenz
Unter der Mengendifferenz von $A$ und $B$ versteht man die Menge aller Elemente, die zwar in $A$ liegen, allerdings nicht in $B$:
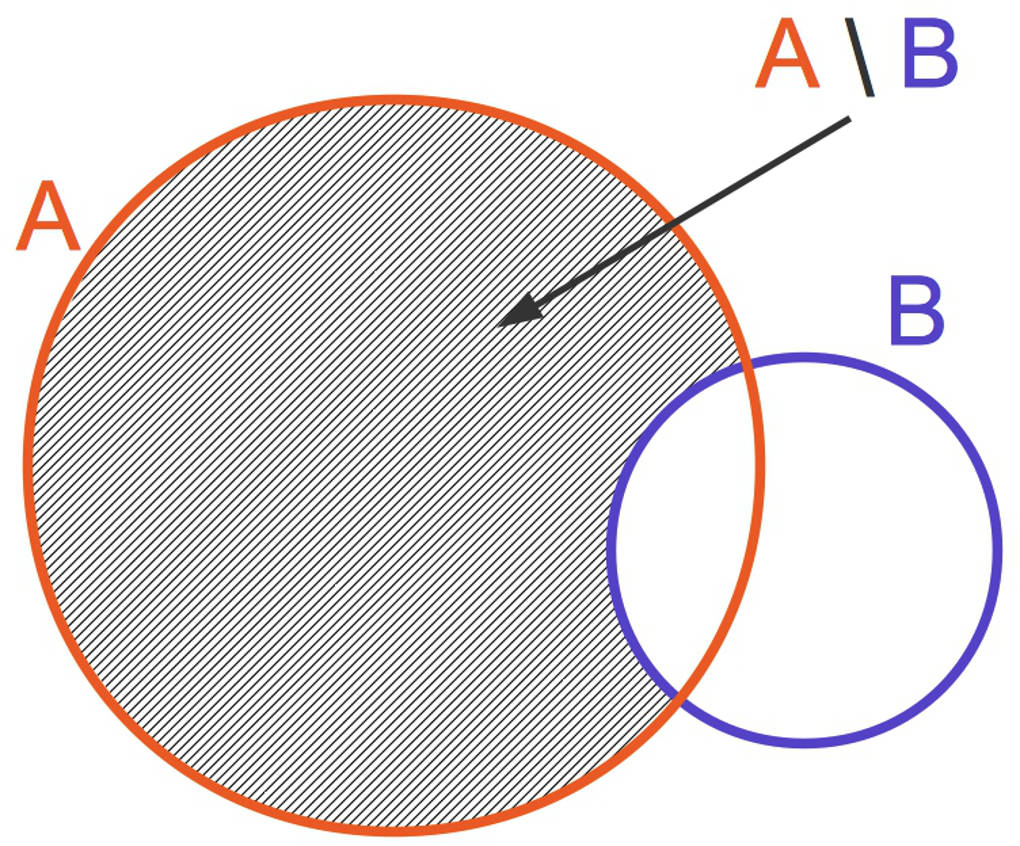
$A\setminus B=\{x~|~x\in A~\text{aber}~x\not\in B\}$.
Beispiel:
- $A=\{1;2;3;4;5;6\}$
- $B=\{4;5;6;7;8;9;10\}$
Dann ist $A\setminus B=\{1;2;3\}$.
Das kartesische Produkt
Das kartesische Produkt zweier Mengen $A$ und $B$ schauen wir uns abschließend noch an einem Beispiel an. Auch das kartesische Produkt ist eine Menge. In dieser befinden sich alle Paare, welche sich ergeben, wenn die eine Koordinate ein Element aus $A$ und die andere ein Element aus $B$ ist:
$A\times B=\{(x|y)~|~x\in A~\text{und}~y\in B\}$.
Beispiel:
- $A=\{1;2;3\}$
- $B=\{0;1\}$
Dann ist $A\times B=\{(1|0);(1|1);(2|0);(2|1);(3|0);(3|1)\}$.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Mengenlehre (3 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Mengenlehre (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter









 Mengen – Einführung
Mengen – Einführung
 Verhältnisse von Mengen – Gleichheit, Teilmengen, elementfremde Mengen
Verhältnisse von Mengen – Gleichheit, Teilmengen, elementfremde Mengen
 Mengenoperationen – Schnitt, Vereinigung, Differenz
Mengenoperationen – Schnitt, Vereinigung, Differenz









