Gebrochenrationale Funktionen – Kurvendiskussion
Definitionsbereich, Wertebereich, Nullstellen, Symmetrie, Extrema, Wendepunkte, Verhalten im Unendlichen, Schnittpunkt y-Achse, Sattelpunkte, Graph, Asymptoten, Polstellen, Polynomdivision mit Rest
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine gebrochenrationale Funktion?
- Der Definitionsbereich einer gebrochenrationalen Funktion
- Nullstellen gebrochenrationaler Funktionen
- Extrema und Wendepunkte gebrochenrationaler Funktionen
- Ausblick
Was ist eine gebrochenrationale Funktion?
Eine gebrochenrationale Funktion $f$ hat die folgende Gestalt:
$f(x)=\dfrac{Z(x)}{N(x)}=\dfrac{a_nx^n+...+a_1x+a_0}{b_mx^m+...+b_1x+b_0}$.
Du siehst, sowohl im Zähler als auch im Nenner steht eine ganzrationale Funktion oder auch ein Polynom. Der Zählergrad ist $n$ und der Nennergrad $m$. Diese müssen nicht übereinstimmen.
Wichtig ist zu beachten, dass eine gebrochenrationale Funktion nicht für alle Zahlen definiert ist. Da die Division durch $0$ nicht erlaubt ist, musst du den Term im Nenner, also $N(x)$, untersuchen. Dieser darf nicht $0$ sein.
Im Folgenden betrachten wir die gebrochenrationale Funktion $f$ mit $f(x)=\frac{x^{2}+1}{x-1}$. Hier ist $Z(x)= x^{2}+1$ ein quadratisches und $N(x)=x-1$ ein lineares Polynom.
Der Definitionsbereich einer gebrochenrationalen Funktion
Um den Definitionsbereich zu bestimmen, berechnest du die Nullstellen des Nennerpolynoms $N(x)$. Diese musst du schließlich ausschließen. Das geht so:
- $N(x)=0$ führt zu $x-1=0$. Addierst du $1$ auf beiden Seiten, erhältst du $x=1$.
- Für diesen $x$-Wert ist die gebrochenrationale Funktion $f$ nicht definiert.
- Das schreibst du so: $\mathbb{D}_{f}=\mathbb{R}\setminus\{1\}$.
$x=1$ wird als Definitionslücke bezeichnet.
Hebbare Definitionslücken
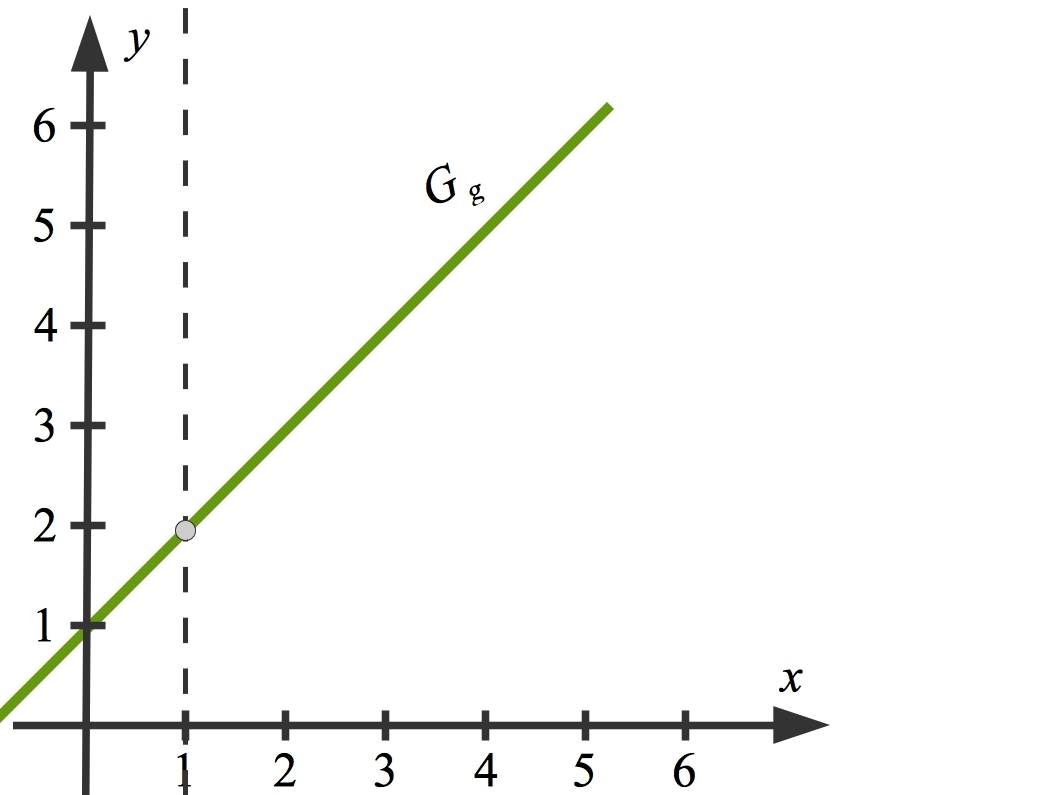
Schaue dir die Funktion $g$ mit $g(x)=\frac{x^{2}-1}{x-1}$ an. Die Definitionslücke ist hier $x=1$. Wenn du genau hinschaust, erkennst du im Zählerpolynom die dritte binomische Formel: $Z(x)=x^{2}-1=(x+1)\cdot (x-1)$.
Du kannst nun kürzen: $g(x)=\frac{x^{2}-1}{x-1}=\frac{(x+1)\cdot (x-1)}{x-1}=x+1$.
Nun ist die Definitionslücke „aufgehoben“. Das stimmt natürlich so nicht: Die Funktion $g$ ist nach wie vor für $x=1$ nicht definiert, jedoch kannst du in der gekürzten Form $x=1$ durchaus einsetzen. Im Funktionsgraphen musst du diese Stelle mit einem kleinen Kreis kennzeichnen.
Nicht hebbare Definitionslücken
Schau dir noch einmal die Funktion $f$ mit $f(x)=\frac{x^{2}+1}{x-1}$ an. Da die Nullstelle des Nennerpolynoms nicht gleichzeitig auch Nullstelle des Zählerpolynoms ist, kannst du nicht kürzen. Das bedeutet, dass die Definitionslücke nicht hebbar ist. Hier liegt, wie im Folgenden abgebildet, eine Polstelle, also eine vertikale Asymptote, vor.
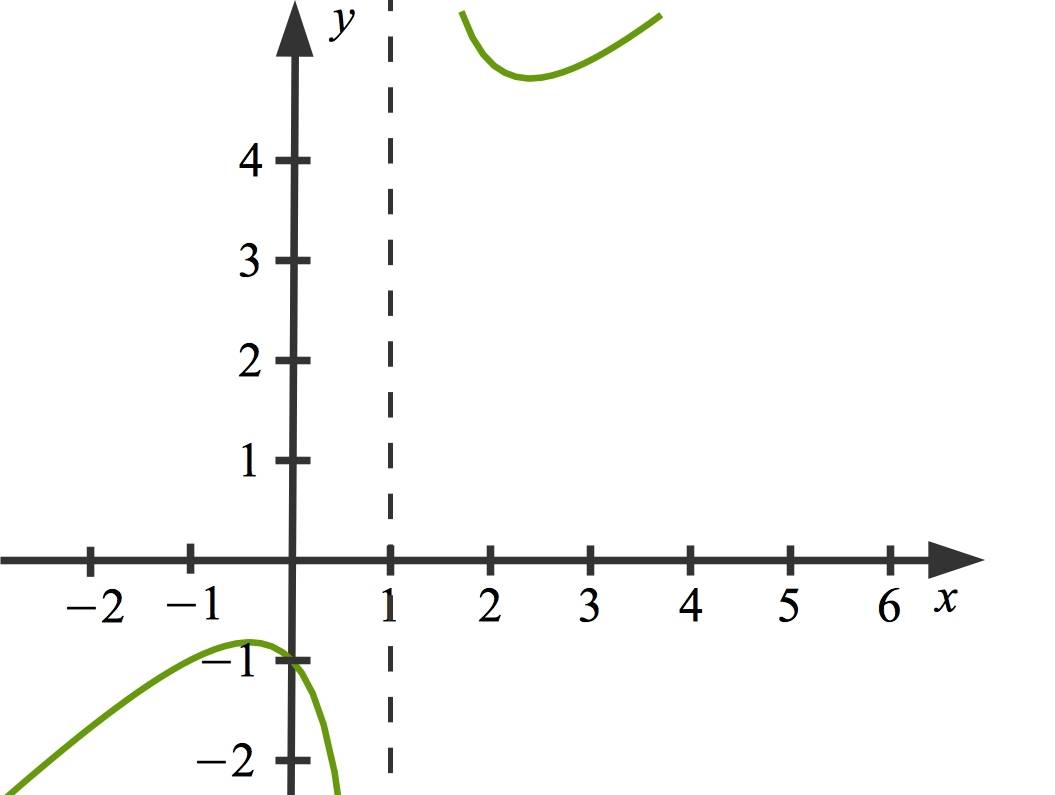
Wir schauen uns nun einmal an, wie eine Kurvendiskussion mit der genannten Funktion $f$ durchgeführt werden kann. An deren Ende steht der hier bereits abgebildete Funktionsgraph.
Nullstellen gebrochenrationaler Funktionen
Möchtest du eine gebrochenrationale Funktion auf Nullstellen untersuchen, genügt es, wenn du den Zähler auf Nullstellen untersuchst. Warum ist das so? Hier siehst du die Begründung:
$\begin{array}{rclll} \dfrac{Z(x)}{N(x)}&=&0&|&\cdot N(x)\\ Z(x)&=&0 \end{array}$
Für die Funktion $f$ folgt also $x^{2}+1=0$. Subtraktion von $1$ auf beiden Seiten der Gleichung führt zu $x^{2}={-1}$. Da die Wurzel aus einer negativen Zahl nicht definiert ist, gibt es keine Lösung dieser Gleichung und damit keine Nullstelle.
Extrema und Wendepunkte gebrochenrationaler Funktionen
Du musst zunächst die ersten beiden (gegebenenfalls sogar die ersten drei) Ableitungen berechnen. Hierfür benötigst du die Quotientenregel. Alternativ kannst du auch eine Polynomdivision durchführen. Bei dieser bleibt bei dem Beispiel der Funktion $f$ ein Rest.
Du erhältst dann $f(x)=x+1+\frac{2}{x-1}$.
Die Funktion $a$ mit $a(x)=x+1$ wird als Asymptotenfunktion bezeichnet. Wenn du den Graphen der Funktion $a$, eine Gerade, in das gleiche Koordinatensystem wie den Funktionsgraphen der Funktion $f$ einzeichnest, siehst du, dass sich der Funktionsgraph dieser Geraden immer weiter annähert. Das bedeutet insbesondere, dass das Grenzwertverhalten der Funktion für $x\to \pm\infty$ mit dem der Geraden übereinstimmt.
Mit Hilfe der obigen Darstellung der Funktion $f$ erhältst du die ersten beiden Ableitungen:
- $f'(x)=1-\frac{2}{(x-1)^{2}}$,
- $f''(x)=\frac{4}{(x-1)^{3}}$.
Nun kannst du bereits erkennen, dass die zweite Ableitung nicht $0$ werden kann, da in ihrem Zähler die $4$ steht. Die Funktion besitzt somit keine Wendepunkte. Du kannst auf die Bestimmung der dritten Ableitung, welche du ausschließlich für den Nachweis der Wendepunkte benötigst, verzichten.
Es bleiben noch die Extrema. Hier muss notwendigerweise gelten, dass $f'\left(x_{E}\right)=0$ ist. Du musst also eine Bruchgleichung lösen.
$\begin{array}{rclll} 1-\frac{2}{(x-1)^{2}}&=&0&|&+\frac{2}{(x-1)^{2}}\\ 1&=&\frac{2}{(x-1)^{2}}&|&\cdot (x-1)^2\\ (x-1)^2&=&2&|&\sqrt{~~~}\\ x-1&=&\pm\sqrt 2&|&+1\\ x&=&1\pm\sqrt 2\\ x_{E_1}&=&1+\sqrt 2\approx2,4\\ x_{E_2}&=&1-\sqrt2\approx-0,4 \end{array}$
Zuletzt prüfst du, ob bei den berechneten $x$-Werten tatsächlich Extrema vorliegen. Hierfür setzt du die beiden gefundenen Lösungen in die zweite Ableitung ein.
- $f''\left(2,4\right)\approx1,5\gt 0$: Das bedeutet, dass hier ein lokales Minimum vorliegt. Zur Berechnung der $y$-Koordinate setzt du $2,4$ in die Funktionsgleichung ein und erhältst $f(2,4)\approx4,8$. Es folgt somit das lokale Minimum $(2,4|4,8)$.
- $f''\left(-0,4\right)\approx-0,3\lt 0$: Hier liegt ein lokales Maximum vor. Berechne noch den zugehörigen Funktionswert: $f(-0,4)\approx-0,8$. Du erhältst somit das lokale Minimum $(-0,4|-0,8)$.
Beide Extrema kannst du der folgenden Darstellung entnehmen.

Ausblick
Wenn du nun noch eine Flächenberechnung durchführen müsstest, könntest du eine Stammfunktion der Funktion $f$ mit Hilfe der Darstellung $f(x)=x+1+\frac2{x-1}$ bestimmen.
Es ist $\int~(x+1)~dx=\frac12x^{2}+x+c$. Eine Stammfunktion des Restes erhältst du mit Hilfe der logarithmischen Integration $\int~\frac2{x-1}~dx=2\ln\left(|x-1|\right)+c$.
Gesamt erhältst du als Stammfunktion $\int~f(x)~dx=\frac12x^{2}+x+2\ln\left(|x-1|\right)+c$.
Alle Videos zum Thema
Videos zum Thema
Gebrochenrationale Funktionen – Kurvendiskussion (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Gebrochenrationale Funktionen – Kurvendiskussion (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter






 Gebrochenrationale Funktionen – Nullstellen
Gebrochenrationale Funktionen – Nullstellen
 Gebrochenrationale Funktionen – Definitionslücken und Asymptoten
Gebrochenrationale Funktionen – Definitionslücken und Asymptoten









