Quadratische Funktionen: f(x) = a · x² + b · x + c
Eine quadratische Funktion in allgemeiner Form kann drei Parameter besitzen, welche jeweils einen anderen Einfluss auf ihren Funktionsgraphen haben.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Allgemeine Form einer quadratischen Funktion
- Merkmale quadratischer Funktionen und ihrer Graphen
- Einfluss des Koeffizienten $a$
- Einfluss des Koeffizienten $b$
- Einfluss des absoluten Gliedes $c$
- Scheitelpunktform
Allgemeine Form einer quadratischen Funktion
Unter einer quadratischen Funktion verstehen wir eine Funktion zweiten Grades folgender Form:
$f(x) = a\cdot x^{2} + b\cdot x + c$
Hierbei handelt es sich um die allgemeine Form, die sich wie folgt zusammensetzt:
- quadratisches Glied $a\cdot x^{2}$
- lineares Glied $b\cdot x$
- absolutes Glied $c$
Da der höchste Exponent einer quadratischen Funktion $2$ ist, gilt $a\neq 0$. Andernfalls würde nämlich das quadratische Glied wegfallen und übrig bliebe die lineare Funktion $f(x) = b\cdot x + c$.
Merkmale quadratischer Funktionen und ihrer Graphen
Der Graph einer quadratischen Funktion ist eine Parabel. Parabeln können unterschiedlich aussehen, was durch die Koeffizienten $a$ und $b$ sowie dem absoluten Glied $c$ verursacht wird.
Einfluss des Koeffizienten $a$
Streckung und Stauchung
Wir betrachten zunächst den Koeffizienten $a$, während wir $b=0$ und $c=0$ annehmen. Der Betrag des Koeffizienten $a$ bestimmt die Breite der Parabel, was man auch als Streckung bzw. Stauchung bezeichnet.
Hat $a$ den Wert $1$, handelt es sich um eine Normalparabel zu der Funktionsgleichung $f(x)=x^2$. Diese ist in der folgenden Abbildung grün dargestellt.
Nun betrachten wir noch zwei Beispielfunktionen und ihre Graphen:
$g(x) = \frac{1}{2}x^2\\ h(x) = 3x^2$
Der Funktionsgraph zu der Funktion $g$ ist im Folgenden rot und der zu $h$ blau dargestellt.
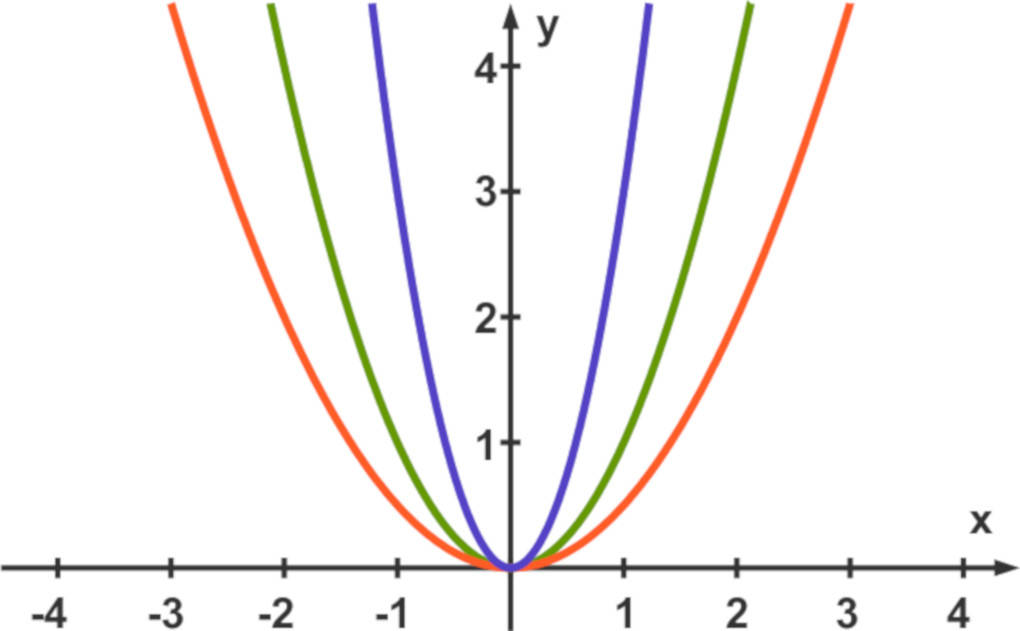
Dieser Abbildung können wir die folgenden Eigenschaften entnehmen:
- $|a|>1$: schmaler als die Normalparabel
- $|a|=1$: Normalparabel
- $0<|a|<1$: breiter als die Normalparabel
Liegt $|a|$ zwischen $0$ und $1$, so ist die Parabel gegenüber der Normalparabel entlang der $y$-Achse gestaucht. Ist $|a|$ größer als $1$, so ist die Parabel gegenüber der Normalparabel entlang der $y$-Achse gestreckt.
Öffnung der Parabel
Der Koeffizient $a$ bestimmt außerdem die Öffnungsrichtung der Parabel.
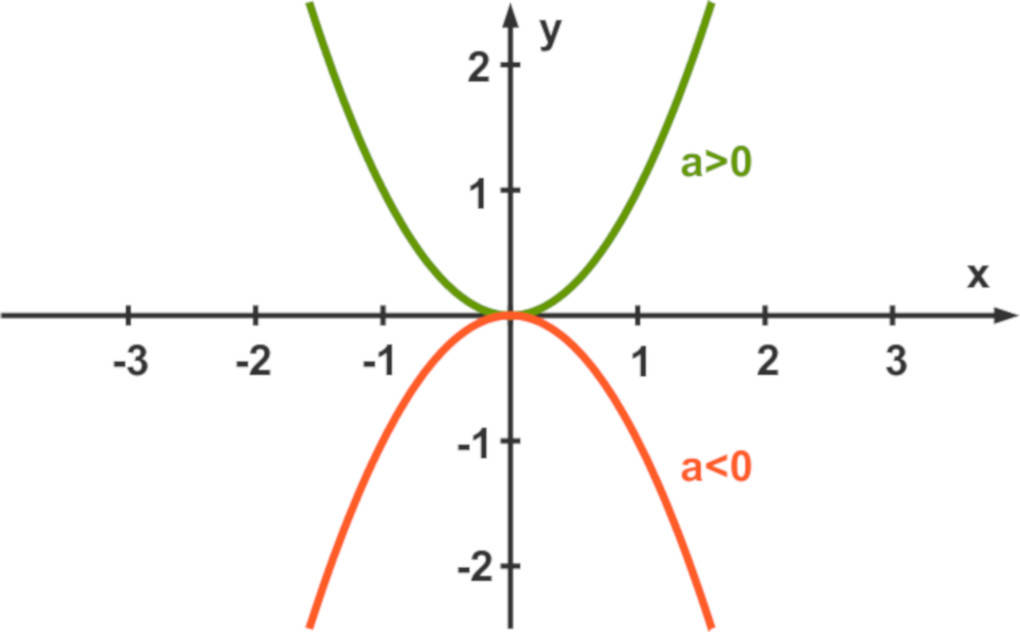
Ist $a$ positiv, ist der Graph nach oben geöffnet. Nimmt $a$ einen negativen Wert an, so ist die Parabel nach unten geöffnet.
Einfluss des Koeffizienten $b$
Der Koeffizient $b$ beeinflusst die Lage des Scheitelpunkts und somit die Lage der Parabel im Koordinatensystem. Durch Variation des Koeffizienten $b$ wird die Parabel entlang der $x$- und $y$-Achse verschoben. Um genau zu sein, wird der Scheitelpunkt der Parabel dadurch entlang einer weiteren Parabel verschoben.
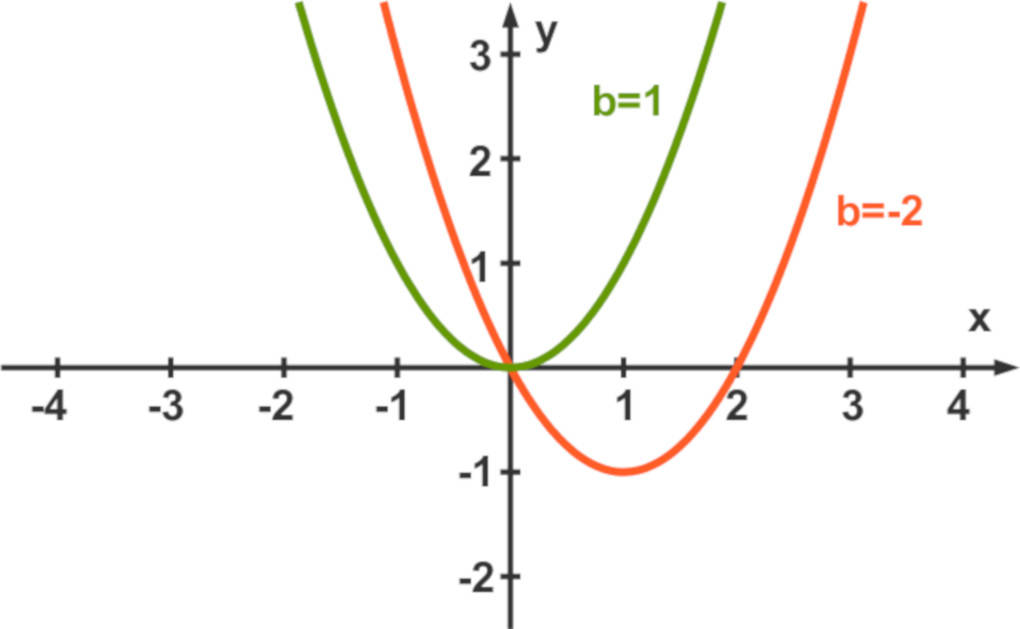
Die Abbildung stellt den Funktionsgraphen zu $f(x)=x^2$ grün und den zu $g(x)=x^2-2x$ rot dar.
Einfluss des absoluten Gliedes $c$
Das absolute Glied $c$ verschiebt den Scheitelpunkt der Parabel entlang der $y$-Achse, also nach oben oder unten. In der folgenden Abbildung sehen wir die Graphen zu den Funktionsgleichungen $f(x)=x^2$ (grün), $g(x)=x^2+1$ (blau) und $h(x)=x^2-2$ (rot).

Scheitelpunktform
Neben der Darstellung in Normalform lässt sich eine quadratische Funktion auch in Scheitelpunktform schreiben. Die Scheitelpunktform lautet allgemein:
$f(x) = a (x - d)^{2} + e$
Der Vorteil ist, dass hieraus der Scheitelpunkt $S (d | e)$ der Parabel sofort abgelesen werden kann.
Eine quadratische Funktion in Normalform lässt sich durch eine quadratische Ergänzung und die erste binomische Formel in die Scheitelpunktform bringen, wie das nachfolgende Beispiel zeigt:
$\begin{array}{lll} f(x) &=& x^2 + 4x + 3 \\ &=& x^2 + 4x + 4 -4+3 \\ &=& (x + 2)^2 - 1 \end{array}$
Den Scheitelpunkt lesen wir ab als $S (-2 | -1)$. Vergleichen wir diese Parabel mit der Normalparabel, die ihren Scheitelpunkt in $S (0 | 0)$ hat, stellen wir fest, dass hier eine Verschiebung um $2$ nach links und $1$ nach unten stattgefunden hat.
Symmetrieachsen
Die Symmetrieachse einer Parabel ist eine Gerade parallel zur $y$-Achse durch den Scheitelpunkt der Parabel.
Wir betrachten hierzu drei Funktionen:
$f(x) = (x - 3)^{2}+2$
Durch die Scheitelpunktform ist der Scheitelpunkt direkt ablesbar als $S (3 | 2)$. Es handelt sich um eine nach oben geöffnete Normalparabel, die um $3$ nach rechts und $2$ nach oben verschoben ist. Die Symmetrieachse verläuft folglich parallel zur $y$-Achse durch den Scheitelpunkt $S$.
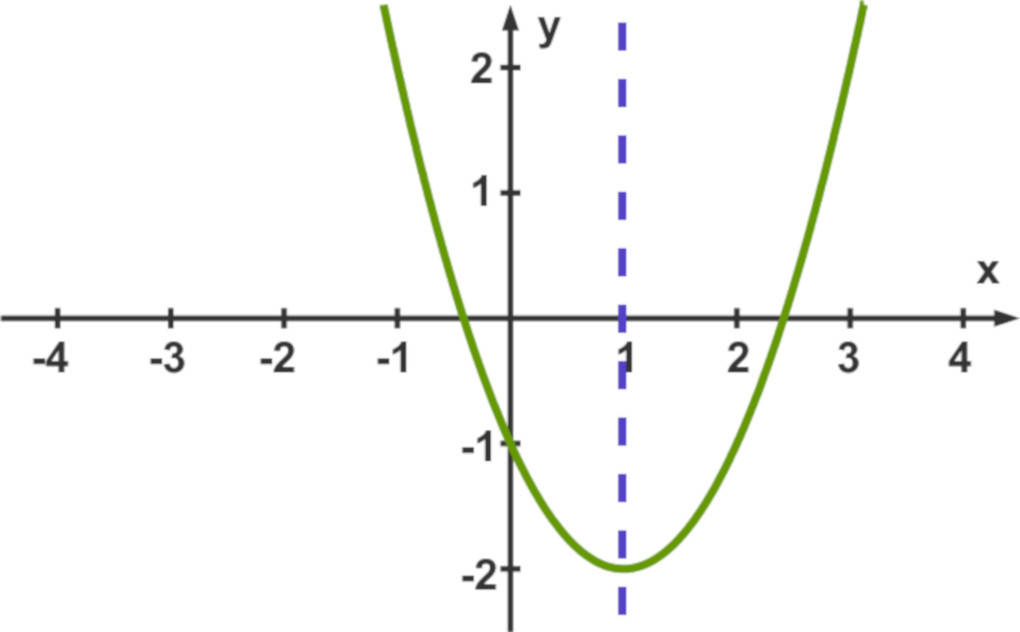
Nun betrachten wir folgende Funktionsgleichung:
$g(x) = -2(x + 1)^{2} - 3$
Die Parabel zu $g$ hat ihren Scheitelpunkt in $S (-1 | -3)$ und ist keine Normalparabel, da vor der Klammer der Faktor $-2$ steht.
Das negative Vorzeichen weist auf eine Öffnung nach unten hin. Der Betrag $2$ zeigt, dass diese Parabel schmaler ist als eine Normalparabel (Streckung). Sie ist zudem um $1$ nach links und um $3$ nach unten verschoben.
Die Symmetrieachse verläuft hier auch parallel zur $y$-Achse durch den Scheitelpunkt $S$.
Das dritte Beispiel ist wie folgt gegeben:
$h(x) = -3x^{2} + 24x - 53$
Hier fällt auf, dass wir von einer Normalform ausgehen. Diese muss zunächst durch Umformungen in die Scheitelpunktform überführt werden:
$\begin{array}{lll} h(x) &=&-3x^2 + 24x - 53 \\ &=& -3(x^2 - 8x) - 53 \\ &=& -3(x^2 - 8x+16-16) - 53 \\ &=& -3(x^2 - 8x+16)+48 - 53 \\ &=& -3(x - 4)^2-5 \end{array}$
Wir können nun den Scheitelpunkt $S (4 |-5)$ ablesen. Außerdem erkennen wir, dass die Parabel schmaler als die Normalparabel und nach unten geöffnet ist. Die Symmetrieachse verläuft parallel zur $y$-Achse durch den Scheitelpunkt $S$.
Vorzeichen der Funktionswerte
Um herauszufinden, in welchen Bereichen sich Funktionswerte von Parabeln befinden, bietet es sich zunächst an, deren Nullstellen zu ermitteln. Dazu betrachten wir folgendes Beispiel:
$\begin{array}{lll} f(x) &=& -0,5x^2 + 2x \\ &=& -0,5(x^2 - 4x) \end{array}$
Die Nullstellen lassen sich bestimmen durch $f(x)=0$:
$\begin{array}{llll} 0&=&-0,5(x^2- 4x) & \vert :(-0,5)\\ 0&=&x^2- 4x & \\ 0&=&x(x- 4) & \end{array}$
Ein Produkt ist dann Null, wenn einer der Faktoren Null ist, also gilt:
$x_1 = 0 \\ x_2 = 4$
Da wir aus dem negativen Koeffizienten $a$ schließen können, dass die Parabel nach unten geöffnet ist, muss der Bereich zwischen den Nullstellen positive Funktionswerte haben. Demnach ist $f(x) \gt 0$ für $0 \lt x\lt 4$.
Alle Videos zum Thema
Videos zum Thema
Quadratische Funktionen: f(x) = a · x² + b · x + c (4 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quadratische Funktionen: f(x) = a · x² + b · x + c (4 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Was sind quadratische Funktionen?
Was sind quadratische Funktionen?
 Quadratische Funktionen – Übersicht
Quadratische Funktionen – Übersicht
 Graphen quadratischer Funktionen
Graphen quadratischer Funktionen
 Nullstellen quadratischer Funktionen berechnen
Nullstellen quadratischer Funktionen berechnen









