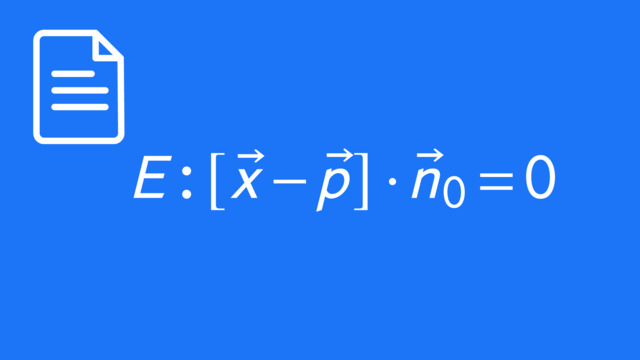Hessesche Normalenform

Die hessesche Normalenform

Du kennst jetzt die Normalenform einer Ebene, aber hast du auch von einer Form der Ebenengleichung gehört, die hessesche Normalenform, Hesse-Normalform oder kurz HNF genannt wird? In diesem Text findest du Beispiele zur Anwendung der hesseschen Normalenform und Schritt-für-Schritt-Anleitungen zur Umwandlung von Ebenengleichungen in die hessesche Normalenform.

Wie ist die hessesche Normalenform aufgebaut?

Die hessesche Normalenform ist ein Spezialfall der Normalenform und wird unter anderem für Abstandsberechnungen verwendet. Die Besonderheit ist, dass der Normalenvektor die Länge $1$ hat. Ein Vektor mit der Länge $1$ wird Einheitsvektor genannt, wir bezeichnen den Normalenvektor daher in diesem Fall als Normaleneinheitsvektor und verwenden das Symbol $n_0$.

Beispiel für eine Ebenengleichung in der hesseschen Normalenform:

$E: \left[\vec x -\begin{pmatrix} 2 \\ -1 \\ 9 \end{pmatrix}\right] \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix} = 0$

Dies ist die Normalenform einer Ebene, die durch den Punkt $P(2\vert -1\vert 9)$ verläuft. Der Vektor

$\vec n_0= \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix} $

steht senkrecht auf der Ebene und hat die Länge $1$. Um die Länge eines Vektors zu bestimmen, berechnen wir seinen Betrag, in diesem Fall gilt:

$\vert \vec n_0 \vert = \sqrt{0,8^2+0^2+0,6^2}=\sqrt{0,64+0+0,36}=1$

Welche Anwendung hat die hessesche Normalenform?

Mithilfe der hesseschen Normalenform kann der Abstand eines Punkts von der Ebene berechnet werden. Dazu setzt man den Ortsvektor des Punkts in die linke Seite der Gleichung für $\vec x$ ein.

Wie bei jeder Normalenform gilt auch bei der hesseschen Normalenform: Wenn $[\vec x - \vec p]\cdot \vec n_0$ null ergibt, liegt der Punkt in der Ebene, denn, wenn das Skalarprodukt null ist, verlaufen die Vektoren $\overrightarrow{PX}$ und $\vec n_0$ senkrecht zueinander. Wenn das Skalarprodukt von null verschieden ist, liegt der Vektor $\overrightarrow{PX}$ nicht rechtwinklig zu $\vec n_0$ und damit der Punkt $X$ außerhalb der Ebene.

Verwenden wir die hessesche Normalenform, enthält das von null verschiedene Ergebnis zusätzlich Informationen über die Lage des Punkts außerhalb der Ebene: Der Betrag des Skalarprodukts gibt den Abstand des Punkts von der Ebene an und das Vorzeichen die Position des Punkts zur Ebene im Vergleich zum Ursprung des Koordinatensystems.

Beispiele für Abstandsberechnungen mit der hesseschen Normalenform:

Gegeben sind die Ebenengleichung

$E: \left[\vec x -\begin{pmatrix} 2 \\ -1 \\ 9 \end{pmatrix}\right] \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix} = 0$

und die Punkte $A(6\vert -1\vert 12)$, $B(5\vert -5\vert 5)$ und $C(-3\vert -5\vert -1)$. Wir setzen nacheinander die Ortsvektoren in die Ebenengleichung ein und bestimmen so jeweils die Lage des Punkts zur Ebene.

$d_A=\left[\begin{pmatrix} 6 \\ -1 \\ 12 \end{pmatrix} -\begin{pmatrix} 2 \\ -1 \\ 9 \end{pmatrix}\right] \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix}= \begin{pmatrix} 4\\ 0 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix}=4\cdot 0,8+3\cdot 0,6=5 $

$\implies$ $A$ liegt $5$ Einheiten von der Ebene entfernt und auf der vom Ursprung abgewandten Seite.

$d_B=\left[\begin{pmatrix} 5\\ -5 \\ 5 \end{pmatrix} -\begin{pmatrix} 2 \\ -1 \\ 9 \end{pmatrix}\right] \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix} = \begin{pmatrix} 3\\ -4 \\-4 \end{pmatrix} \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix}=3\cdot 0,8-4\cdot 0,6=0$

$\implies$ $B$ liegt in der Ebene.

$d_C=\left[\begin{pmatrix} -3 \\ -5 \\ -1 \end{pmatrix} -\begin{pmatrix} 2 \\ -1 \\ 9 \end{pmatrix}\right] \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix} =\begin{pmatrix} -5\\ -4 \\ -10 \end{pmatrix} \cdot \begin{pmatrix} 0,8 \\ 0 \\ 0,6 \end{pmatrix}= -5\cdot ,8-10\cdot 0,6=-10$

$\implies$ $C$ liegt $10$ Einheiten von der Ebene entfernt und auf der gleichen Seite wie der Ursprung.

Wie kann man eine Ebenengleichung in die hessesche Normalenform umwandeln?

Jede Ebenengleichung kann in die hessesche Normalenform umgewandelt werden. Je nachdem in welcher Form die Ebenengleichung vorliegt, müssen verschiedene Rechenschritte durchgeführt werden, um die hessesche Normalenform zu bilden.

Von der Normalenform in die hessesche Normalenform

Gegeben ist eine Ebene in Normalenform:

$E: \left[\vec x -\begin{pmatrix} 3 \\ 1 \\ 5 \end{pmatrix}\right] \cdot \begin{pmatrix} 8 \\ 1 \\ 4 \end{pmatrix} = 0$

Um aus dieser Ebene eine hessesche Normalenform herzustellen, muss zunächst die Normierung des Normalenvektors vorgenommen werden, sodass er die Länge $1$ hat. Dazu berechnen wir zunächst die Länge von $\vec n$:

$\vert \vec n_0\vert=\sqrt{8^2+1^2+4^2}=\sqrt{64+1+16}=\sqrt{81}=9$

Wenn man eine Länge von $9$ Einheiten durch $9$ dividiert, erhält man die Länge $1$. In der Vektorrechnung ist die Division nicht definiert, daher multiplizieren wir den Vektor mit dem Kehrwert:

$n_0= \frac{1}{9}\cdot \begin{pmatrix} 8 \\ 1 \\ 4 \end{pmatrix} =\begin{pmatrix} \frac{8}{9} \\ \\ \frac{1}{9} \\ \\ \frac{4}{9} \end{pmatrix} $

Den so erhaltenen Normaleneinheitsvektor setzen wir anstelle des vorherigen Normalenvektors in die Normalenform ein und erhalten so die hessesche Normalenform:

$E: \left[\vec x -\begin{pmatrix} 3 \\ 1 \\ 5 \end{pmatrix}\right] \cdot \frac{1}{9}\cdot \begin{pmatrix} 8 \\ 1 \\ 4 \end{pmatrix} = 0$

Von der Parameterform in die hessesche Normalenform

Gegeben ist eine Ebene in Parameterform:

$E: \vec x = \begin{pmatrix} 1 \\ 1\\ 0 \end{pmatrix}+ r\cdot \begin{pmatrix} 2\\ 1 \\ 2 \end{pmatrix} + s\cdot \begin{pmatrix} 0 \\ 4\\ 0 \end{pmatrix}$

Wir bestimmen als Erstes einen Normalenvektor, der senkrecht auf den beiden Spannvektoren steht, und verwenden dazu das Kreuzprodukt:

$\vec n= \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \times \begin{pmatrix} 0 \\ -4\\ 0 \end{pmatrix} =\begin{pmatrix} 8 \\ 0 \\ -8 \end{pmatrix}$

Anschließend bestimmen wir die Länge des Vektors und verwenden dazu den Betrag:

$\vert \vec n \vert = \sqrt{8^2+0^2+(-8)^2}=\sqrt{64+0+64}=\sqrt{128}.$

Somit können wir den Normaleineinheitsvektor bestimmen:

$n_0= \frac{1}{\sqrt{128}}\cdot \begin{pmatrix} 8 \\ 0 \\ -8 \end{pmatrix}$

Den Stützvektor $P(1\vert 1\vert 0)$ können wir aus der Parameterform ablesen und abschließend mithilfe des Normaleneinheitsvektors und des Stützvektors die hessesche Normalenform angeben:

$E: \left[\vec x -\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\right] \cdot \frac{1}{\sqrt{128}}\cdot \begin{pmatrix} 8 \\0 \\ -8 \end{pmatrix} = 0$

Von der Koordinatenform in die hessesche Normalenform

Gegeben ist eine Ebene in Koordinatenform:

$E: 2x_1+2x_2+x_3= 21$

Als Erstes können wir einen Normalenvektor ablesen:

$\vec n= \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}$

Anschließend bestimmen wir die Länge des Vektors:

$\vert \vec n \vert = \sqrt{2^2+2^2+1^2}=\sqrt{4+4+1}=\sqrt{9}=3$

Somit können wir den Normaleneinheitsvektor bestimmen:

$n_0= \frac{1}{3}\cdot \begin{pmatrix} 2\\ 2 \\ 1 \end{pmatrix}$

Anschließend müssen wir einen Punkt finden, der auf der Ebene liegt. Dazu setzen wir Werte für die Koordinaten ein, sodass die Gleichung erfüllt ist. Für $x_1=0$, $x_2=0$ und $x_3=21$ ist die Gleichung $2x_1+2x_2+x_3= 21$ erfüllt, denn $2\cdot 0+2\cdot 0+1\cdot 21=21$. Daher liegt $(0\vert 0\vert 21)$ in der Ebene und sein Ortsvektor kann als Stützvektor verwendet werden.

Also können wir die hessesche Normalenform angeben:

$E: \left[\vec x -\begin{pmatrix} 0 \\ 0 \\ 21 \end{pmatrix}\right] \cdot \frac{1}{3}\cdot \begin{pmatrix} 2 \\2 \\ 1 \end{pmatrix} = 0$