Sattelpunkt berechnen

Was ist ein Sattelpunkt? – Definition

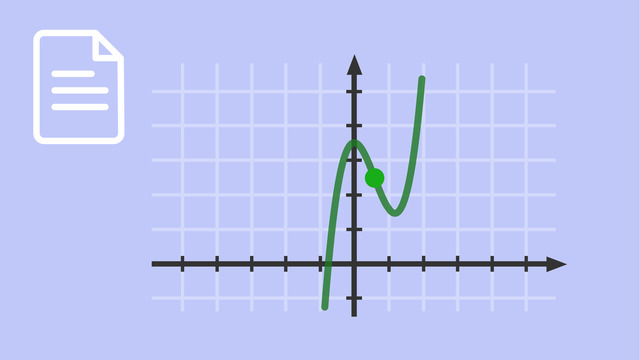
Ein Sattelpunkt ist ein charakteristischer Punkt, den einige Funktionsgraphen besitzen. Genau wie Extrempunkte und Wendepunkte müssen Sattelpunkte häufig im Rahmen einer Kurvendiskussion bestimmt werden. Sattelpunkte werden auch als Terrassenpunkte oder Horizontalwendepunkte bezeichnet und sind Wendepunkte mit der Steigung null, also Spezialfälle des Wendepunkts.

An einem Sattelpunkt verläuft die Tangente waagerecht zur $x$-Achse, also ist die erste Ableitung an dieser Stelle gleich null. Dennoch handelt es sich aber nicht um ein Minimum oder Maximum. In der Umgebung eines Sattelpunkts ist der Funktionsgraph monoton steigend oder monoton fallend (allerdings nicht streng monoton steigend bzw. fallend), es findet kein Vorzeichenwechsel der ersten Ableitung statt. Da es sich um einen Wendepunkt handelt, ändert sich jedoch das Krümmungsverhalten von rechtsgekrümmt nach linksgekrümmt oder andersherum.

Wie der Name schon sagt, erinnert das Aussehen des Graphen an dieser Stelle an einen Sattel (oder eine Terrasse).

Sattelpunkt bestimmen – Vorgehensweisen

Ähnlich wie bei Extrempunkten und Wendepunkten gibt es keine Formel zur Berechnung des Sattelpunkts. Er muss in mehreren Schritten bestimmt werden. Es kommen zwei verschiedene Verfahren zum Einsatz, je nachdem welches Vorwissen du bereits im Unterricht erworben hast.

Bei dem ersten Verfahren wird nur die erste Ableitung benötigt. Es kann bei allen Polynomfunktionen angewendet werden.

Bei dem zweiten Verfahren werden auch die höheren Ableitungen benötigt.

Für beide Verfahren schauen wir uns zuerst eine Schritt-für-Schritt-Anleitung an und berechnen dann Beispielaufgaben.

Sattelpunkt berechnen – mit dem Vorzeichenwechselkriterium

Unsere Beispielfunktion lautet $f(x)=x^3$. Bestimme die Sattelpunkte – falls es welche gibt!

Wir bestimmen in dieser Beispielaufgabe den Sattelpunkt mit dem Vorzeichenwechselkriterium nach der obigen Schritt-für-Schritt-Anleitung.

1. Ableitung bestimmen

$f(x)=x^3$

$f^{\prime}(x)=3x^2$

2. Nullstelle der Ableitung bestimmen

$f^{\prime}(x)=0\implies 3x^2=0$

Die Lösung der Gleichung ist $x=0$ und an dieser Stelle hat der Graph eine waagerechte Tangente. Damit ist die notwendige Bedingung für Extrempunkte, aber auch die notwendige Bedingung für Sattelpunkte erfüllt.

3. VZW an der Stelle $x=0$ prüfen

Es muss eine Zahl größer und eine Zahl kleiner als null in die erste Ableitung eingesetzt werden. Die Zahlen sind beliebig, wir verwenden $-1$ und $1$, weil sich damit einfach rechnen lässt.

$f^{\prime}(-1)=3\cdot (-1)^2=3 \implies f^{\prime}(-1)>0 \implies f \text{ ist steigend }$

$f^{\prime}(1)=3\cdot 1^2=3 \implies f^{\prime}(1)>0 \implies f \text{ ist steigend }$

Der Graph ist also vor und nach der Stelle mit der waagerechten Tangente steigend. Es kann sich nicht um einen Extrempunkt handeln. Daher liegt ein Sattelpunkt an der Stelle $x=0$ vor.

4. $y$-Koordinate berechnen

Da wir den $x$-Wert des Sattelpunkts kennen, müssen wir nur noch die $y$-Koordinate durch Einsetzen in die ursprüngliche Funktion bestimmen:

$f(0)=0^3=0$.

Die Funktion $f(x)=x^3$ hat einen Sattelpunkt bei $(0\vert 0)$.

Sattelpunkt berechnen – mit den höheren Ableitungen

Unsere Beispielfunktion lautet $f(x)=-x^4+6x^2+8x+7$. Bestimme die Sattelpunkte – falls es welche gibt!

Wir bestimmen in dieser Beispielaufgabe den Sattelpunkt mit den hinreichenden Bedingungen nach der obigen Schritt-für-Schritt-Anleitung.

1. Ableitungen bestimmen

$f(x)=x^4-6x^2-8x+7$

$f^{\prime}(x)=4x^3-12x-8$

$f^{\prime\prime}(x)=12x^2-12$

$f^{\prime\prime\prime}(x)=24x$

2. Nullstellen der zweiten Ableitung bestimmen

$f^{\prime\prime}=0\implies 12x^2-12=0\implies x^2=1 \implies x_1=1 \text{ und } x_2=-1$

3. Bedingungen prüfen

Wir prüfen zuerst die dritte Ableitung:

$f^{\prime\prime\prime}(1)=24\cdot 1=24 \implies f^{\prime\prime\prime}(1)\neq 0$

$f^{\prime\prime\prime}(1)=24\cdot (-1)=24 \implies f^{\prime\prime\prime}(-1)\neq 0$

Bei $x_1=1$ und $x_2=-1$ liegen also Wendepunkte vor.

Danach prüfen wir die erste Ableitung:

$f^{\prime}(1)=4\cdot 1^3-12\cdot 1-8=-16 \implies f^{\prime}(1)\neq 0$

$f^{\prime}(-1)=4\cdot (-1)^3-12\cdot (-1)-8=0 \implies f^{\prime}(-1)=0$

Damit liegt an der Stelle $x_1=1$ ein „normaler“ Wendepunkt vor und an der Stelle $x_2=-1$ ein Sattelpunkt.

4. Berechnung der $y$-Koordinate

$f(x)=(-1)^4-6\cdot(-1)^2-8\cdot (-1)+7=4$.

Der Sattelpunkt liegt bei $(-1\vert 4)$.

Vergleich der beiden Verfahren zur Bestimmung des Sattelpunkts

Du hast zwei Verfahren kennengelernt, um den Sattelpunkt zu bestimmen. Wenn du bereits die höheren Ableitungen kennst, wirst du meistens das zweite Verfahren anwenden. Es ist zeitsparender, insbesondere wenn nicht nur die Sattelpunkte gesucht werden, sondern eine vollständige Kurvendiskussion durchgeführt werden soll und auch die Wendepunkte gesucht werden.

Allerdings ist zu beachten, dass es sich bei den Bedingungen nur um hinreichende Bedingungen handelt, die aber keine notwendigen Bedingungen sind. Das heißt, wenn $f^{\prime}(x_S)= 0$ und $f^{\prime\prime}(x_S)= 0$ und $f^{\prime\prime\prime}(x_S)\neq 0$ gilt, liegt ein Sattelpunkt vor.

Falls aber die dritte Bedingung nicht erfüllt ist, also $f^{\prime\prime\prime}(x_S)= 0$ gilt, kann man daraus nicht schließen, dass kein Sattelpunkt vorliegt. In dem Fall muss man das Vorzeichenwechselkriterium überprüfen, um eine Antwort zu erhalten.

Zur Verdeutlichung schauen wir uns ein letztes Beispiel an:

Bestimme die Sattelpunkte der Funktion $f(x)=-x^5+3$.

Wir wenden zunächst das zweite Verfahren an.

Dazu bestimmen wir die ersten drei Ableitungen:

$f^{\prime}(x)=-5x^4$

$f^{\prime\prime}(x)=-20x^3$

$f^{\prime\prime\prime}(x)=-60x^2$

Danach bestimmen wir die Nullstelle der zweiten Ableitung:

$f^{\prime\prime}(x)=0 \implies -20x^3=0\implies x=0$

Setzen wir die Nullstelle der zweiten Ableitung in die dritte Ableitung ein, erhalten wir

$f^{\prime\prime\prime}(0)=-60\cdot0^2=0$

Also können wir mithilfe des zweiten Verfahrens keine Aussage über die Existenz eines Wendepunkts oder Sattelpunkts treffen.

Daher gehen wir zum ersten Verfahren über und bestimmen die Nullstellen der ersten Ableitung:

$f^{\prime}(x)=0\implies -5x^4=0\implies x=0$

Anschließend überprüfen wir den Vorzeichenwechsel der ersten Ableitung:

$f^{\prime}(-1)=- 5\cdot(-1)^4=0 =-5$

$f^{\prime}(1)=- 5\cdot 1^4=0 =-5$

Es gibt keinen Vorzeichenwechsel, der Graph ist vor und nach der Stelle mit der waagerechten Tangente fallend. Es liegt ein Sattelpunkt bei $x=0$ vor, dessen $y$-Koordinate durch Einsetzen in den Funktionsterm bestimmt werden kann:

$f(0)=-0^5+3=3$

Der Sattelpunkt liegt bei $(0\vert 3)$.

Häufig gestellte Fragen zum Thema Sattelpunkt berechnen