Ganze Zahlen – Grundrechenarten
Wenn du von einer größeren natürlichen Zahl eine kleinere subtrahierst 7-4=3, erhältst du wieder eine natürliche Zahl. Umgekehrt 4-7=-3 erhältst du eine negative Zahl. Die natürlichen Zahlen gemeinsam mit den negativen Zahlen sind die ganzen Zahlen.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Zahlenbereiche
- Die ganzen Zahlen
- Darstellung von ganzen Zahlen an dem Zahlenstrahl
- Rechnen mit ganzen Zahlen
- Die Anordnung von ganzen Zahlen
- Welche Zahlenbereiche gibt es noch?
Zahlenbereiche
Die ganzen Zahlen stellen einen Zahlenbereich in der Mathematik dar. Es gibt verschiedene Zahlenbereiche.
Die natürlichen Zahlen
Ganz früh lernst du in der Schule den natürlichen Zahlenbereich $(\mathbb{N})$ kennen. Natürliche Zahlen helfen uns beim Zählen: Du kannst zum Beispiel zählen, wie viele Stück Kuchen an deinem Geburtstag gegessen werden oder wie viele Hunde du auf einem Spaziergang triffst.
Mathematisch kannst du die natürlichen Zahlen so aufschreiben:
$\mathbb{N}=\{0;1;2;3;4;...\}$
Wenn du
- zwei natürliche Zahlen addierst, zum Beispiel $7+5=12$, oder
- von einer größeren natürlichen Zahl eine kleinere natürliche Zahl subtrahierst, $23-8=15$,
erhältst du wieder eine natürliche Zahl.
Weshalb müssen die Zahlenbereiche erweitert werden?
Vor langer Zeit haben die Menschen nur mit natürlichen Zahlen gerechnet. Doch sie fanden Aufgaben, die sie nicht lösen konnten. Wenn du von einer natürlichen Zahl eine größere natürliche Zahl subtrahierst, zum Beispiel $3-7=-4$, dann ist das Ergebnis keine natürliche Zahl. Deswegen haben sich die Mathematiker und Mathematikerinnen besprochen und weitere Zahlen erfunden, mit denen man solche Aufgaben lösen kann. Diese neue erfundenen Zahlen nannten sie negative Zahlen. Die negativen Zahlen und die natürlichen Zahlen zusammen nannten sie ganze Zahlen.
Deswegen lernst du nach und nach neue Zahlenbereiche kennen.
Die ganzen Zahlen
Die Zahl $-4$ ist keine natürliche Zahl. Die Zahl $-4$ ist allerdings eine ganze Zahl: Die ganzen Zahlen $(\mathbb{Z})$ setzen sich aus den natürlichen Zahlen und den negativen Zahlen zusammen.
Mathematisch schreibt man die ganzen Zahlen so auf:
$\mathbb{Z}=\{...;-4;-3;-2;-1;0;1;2;3;4;...\}$
Das heißt, dass jede natürliche Zahl auch eine ganze Zahl ist.
Wenn du dir die ganzen Zahlen anschaust, erkennst du, dass zu jeder natürlichen Zahl $1$, $2$, ... auch deren Gegenzahl, also die Zahl mit einem Minuszeichen davor, $-1$, $-2$, ... zu den ganzen Zahlen gehört. Übrigens ist die Gegenzahl von $0$ wieder $0$.
Schauen wir uns Beispiele für ganze Zahlen an:
Tordifferenz
Deine liebste Fußballmannschaft hat in einer Saison $45$ Tore geschossen. Leider haben die gegnerischen Mannschaften gegen deine Lieblingsmannschaft insgesamt $62$ Tore geschossen: Dies führt zu einer negativen Tordifferenz $45-62=-17$. Dass vor der Zahl $17$ ein Minuszeichen steht, bedeutet, dass deine Lieblingsmannschaft mehr Tore kassiert hat, als sie selbst geschossen hat.
Temperaturen
Heute zeigt das Thermometer $26^\circ C$ an. Der Gefrierpunkt liegt bei $0^\circ C$. Manchmal ist es auch sehr kalt, dann zeigt das Thermometer Minusgrade an. Vielleicht hast du im Winter schon einmal gelesen, dass die Temperatur bis auf $-15^\circ C$ sinkt.
Darstellung von ganzen Zahlen an dem Zahlenstrahl
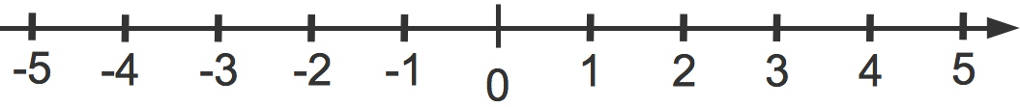
Hier siehst du die Zahlen von $-5$ bis $5$ auf einem Zahlenstrahl. In der Mitte siehst du die $0$. Die $0$ trennt die negativen Zahlen von den natürlichen Zahlen:
- Die natürlichen Zahlen $1$ bis $5$ werden rechts von der $0$ eingezeichnet und
- die negativen Zahlen auf der Zahlengeraden ($-1$ bis $-5$) stehen links von der $0$.
Rechnen mit ganzen Zahlen
Addition und Subtraktion
Hier lernst du, wie du mit ganzen Zahlen und somit auch mit negativen Zahlen rechnen kannst. Wir schauen uns einige Beispiele an:
Wenn du von einer negativen Zahl eine andere negative Zahl subtrahierst, kannst du dir dies wieder an einem Zahlenstrahl klarmachen.
Nehmen wir die Aufgabe: $-2-3=-5$.
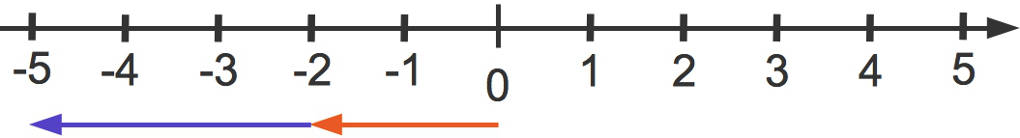
Du startest immer bei der $0$. Die erste Zahl $-2$ bedeutet, dass du zwei Schritte nach links gehen musst. Das ist im Zahlenstrahl als roter Pfeil eingezeichnet. Die Zahl $-3$ bedeutet, dass du drei Schritte weiter nach links gehen musst. Das ist im Zahlenstrahl als blauer Pfeil eingezeichnet. Wenn wir den roten und den blauen Pfeil nach links gegangen sind, kommen wir bei der Zahl $-5$ an. Das Ergebnis der Aufgabe $-2-3$ ist also $-5$.
Hier siehst du weitere Rechenbeispiele:
$\begin{array}{lllll} -4+6&=&2 && \\ 8-10&=&-2 && \\ -2-3+4&=&-5+4 &=& -1 \end{array}$
Rechne von links nach rechts.
Der Betrag einer ganzen Zahl
Der Betrag einer (ganzen) Zahl ist der Abstand dieser Zahl von $0$ am Zahlenstrahl. Mathematisch kann man das so aufschreiben:
$|z| = \begin{cases} & z\text{, für }z\ge 0 \\ & -z\text{, für }z \lt 0 \end{cases}$
Beispiele:
$\quad$ $|4|=4$ Du siehst, bei einer natürlichen Zahl ist der Betrag der Zahl die Zahl selbst.
$\quad$ $|-7|=7$ Bei einer negativen Zahl ist der Betrag der Zahl deren Gegenzahl.
Multiplikation und Division
Du hast sicherlich schon einmal gehört, dass Minus mal Minus gleich Plus ist. Es gilt zusätzlich, dass Plus mal Minus gleich Minus und ebenso Minus mal Plus gleich Minus ist. Die gleichen Regeln kannst du dir für die Division einprägen.
Wenn du also zwei ganze Zahlen multiplizierst oder dividierst, kannst du die Beträge der Zahlen multiplizieren oder dividieren und dann nach den oben genannten Regel ein Minuszeichen, sofern nötig, vor das Ergebnis schreiben:
$\begin{array}{lll} -3\cdot (-4) &=& 12 \\ 2\cdot (-5) &=& -10 \\ {-20}:{(-5)} &=& 4 \\ {12}:{(-6)} &=& -2 \end{array}$
Die Anordnung von ganzen Zahlen
Die Anordnung von ganzen Zahlen kannst du dir wieder an einem Zahlenstrahl klarmachen.
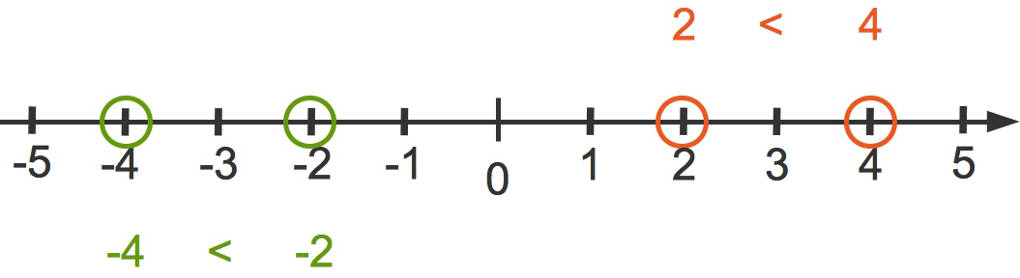
Jede negative Zahl ist kleiner als jede natürliche Zahl:
$\begin{array}{lll} -4 & \lt & 2 \\ -3 & \lt & 0 \\ -7 & \lt & 7 \end{array}$
Im Bereich der natürlichen Zahlen ist $2$ kleiner als $4$, also $2<4$. Wenn du die Gegenzahlen von $2$ und $4$ betrachtest, dreht sich das Relationszeichen um: Hier ist $-2$ größer als $-4$, also $-2>-4$. Das liegt daran, dass $-2$ auf dem Zahlenstrahl rechts von $-4$ steht.
Welche Zahlenbereiche gibt es noch?
Vielleicht hast du dir schon gedacht, dass es auch andere Aufgaben gibt, die du nicht mithilfe der ganzen Zahlen lösen kannst. Zum Beispiel die Aufgabe $5:2$. Da die $5$ keine gerade Zahl ist, ist das Ergebnis dieser Aufgabe mit Sicherheit keine ganze Zahl. Die Lösung der Aufgabe finden wir im Zahlbereich der rationalen Zahlen.
Die rationalen Zahlen werden mathematisch so aufgeschrieben:
$\mathbb{Q}=\left\{\frac ab;~a\in\mathbb{Z};~b\in \mathbb{N};~b\neq 0\right\}$.
Im Alltag sagen wir zu den Zahlen, die hier dazu kommen, Brüche. Wenn wir von rationalen Zahlen sprechen, dann sprechen wir von Brüchen, negativen und natürlichen Zahlen.
Und damit nicht genug: Es gibt noch weitere Zahlbereiche, die noch mehr möglich machen.
Alle Videos zum Thema
Videos zum Thema
Ganze Zahlen – Grundrechenarten (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Ganze Zahlen – Grundrechenarten (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter










 Ganze Zahlen – Grundrechenarten
Ganze Zahlen – Grundrechenarten
 Ganze Zahlen addieren
Ganze Zahlen addieren
 Ganze Zahlen multiplizieren
Ganze Zahlen multiplizieren
 Mit negativen Zahlen rechnen
Mit negativen Zahlen rechnen
 Negative Zahlen addieren und subtrahieren
Negative Zahlen addieren und subtrahieren









