Parameter

Inhaltsverzeichnis zum Thema

• Was ist eine Variable?
• Was ist ein Parameter?
• Die Bedeutung von Parametern
• Parameter am Beispiel von verschiedenen Funktionen
• Lineare Funktionen
• Quadratische Funktionen
• Eponentialfunktionen

Was ist eine Variable?

Eine Variable ist ein Kleinbuchstabe, der als Platzhalter verwendet wird. Häufig verwenden wir den Buchstaben $x$. Der Begriff „Variable“ kommt vom lateinischen Adjektiv „variabilis“, welches übersetzt „veränderlich“ bedeutet. Eine Variable kann also als Veränderliche bezeichnet werden. Mit Variablen kannst du Zusammenhänge allgemein darstellen.

Was ist ein Parameter?

Parameter werden auch Formvariablen genannt. Sie treten in Funktionsgleichungen gemeinsam mit den Variablen $x$ oder $y$ auf, sind aber von anderer Qualität. Parameter sind beliebig wählbar, jedoch im Gegensatz zu den Argumenten $x$ und $y$ für konkrete Funktionsgleichungen fest.

Was bedeutet dies?

• Wenn eine Variable $x$ sich ändert, ändert sich in Abhängigkeit davon auch der Funktionswert $y$.
• Ein fest gewählter Parameter bleibt für die entsprechende Funktionsgleichung immer gleich.

Die Bedeutung von Parametern

Wir benennen im Folgenden unseren Parameter mit $p$. Dieser kann die Funktion an verschiedenen Stellen beeinflussen:

$f(x)+p$ beschreibt die Addition einer Zahl zu dem Funktionswert. Dies führt zu einer Verschiebung entlang der y-Achse.

• Für $p>0$ wird der Funktionsgraph um $p$ Einheiten nach oben und
• für $p<0$ um $p$ Einheiten nach unten verschoben.

$f(x+p)$ beschreibt die Addition einer Zahl zu dem Argument $x$ der Funktion. Dies führt zu einer Verschiebung entlang der x-Achse.

• Für $p>0$ wird der Funktionsgraph um $p$ Einheiten nach links und
• für $p<0$ um $p$ Einheiten nach rechts verschoben.

$p\cdot f(x)$ beschreibt das Multiplizieren des Funktionswertes mit einem Parameter: Dies führt zu einer Streckung bzw. Stauchung des Funktionsgraphen entlang der y-Achse. Für negative $p$ wird die Funktion auch an der x-Achse gespiegelt.

$f(p\cdot x)$ beschreibt das Multiplizieren des Argumentes mit einem Parameter. Dies führt zu einer Streckung bzw. Stauchung des Funktionsgraphen entlang der x-Achse.

Parameter am Beispiel von verschiedenen Funktionen

Lineare Funktionen

Wir wollen Parameter noch besser verstehen. Dazu betrachten wir die üblichen Funktionsarten. Beginnen wir mit einer linearen Funktion der Form $f(x)=mx+n$ mit den Parametern $m$ und $n$. Du weißt bereits, dass $m$ für die Steigung einer linearen Funktion und $n$ für den y-Achsenabschnitt der linearen Funktion stehen. Der Funktionsgraph einer linearen Funktion ist eine Gerade.

• Wenn die Steigung $m$ positiv (negativ) ist, steigt (fällt) die Gerade.
• Je größer die Steigung im Betrag ist, desto steiler ist die Gerade.
• Der y-Achsenabschnitt $n$ ist die Stelle, an welcher die Gerade die y-Achse schneidet.

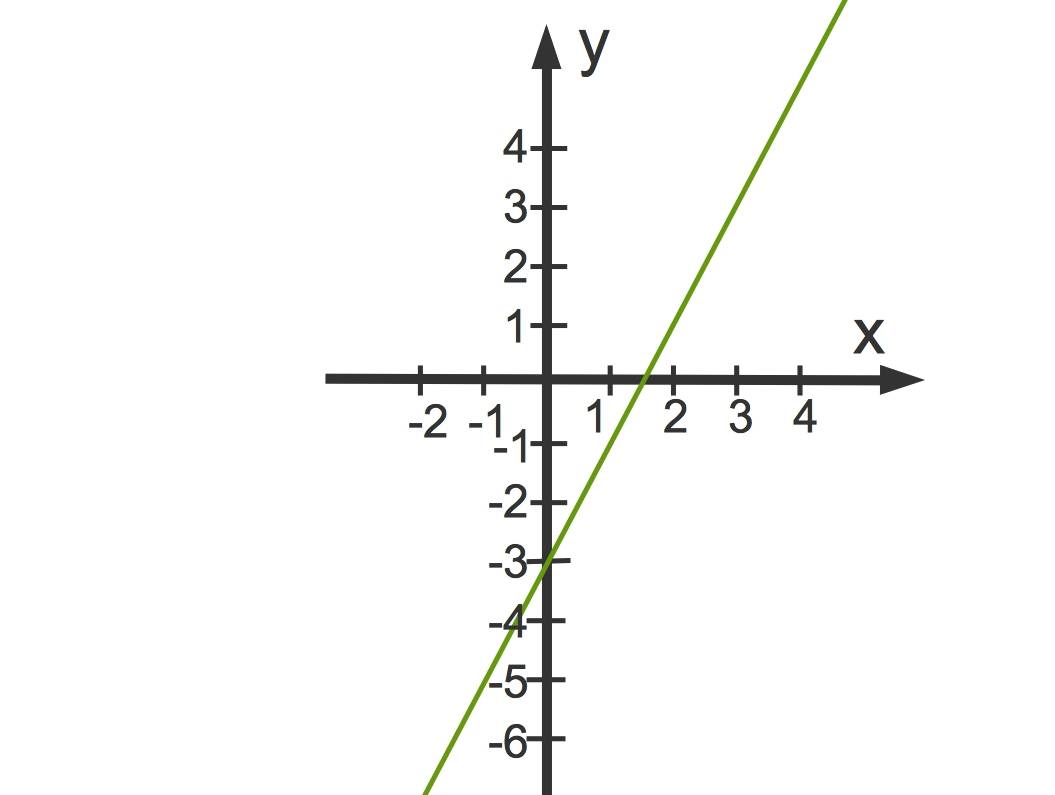
Hier ist der Graph der Funktion $f(x)=2x-3$ zu sehen. Bei $y=n=-3$ wird die y-Achse geschnitten. Die Steigung $m=2$ kannst du auch ablesen: ein Schritt nach rechts, zwei Schritte nach oben.

Quadratische Funktionen

Eine quadratische Funktion kann in allgemeiner Form

$f(x)=ax^2+bx+c$

oder in Scheitelpunktform

$f(x)=a(x-d)^2+e$

gegeben sein. Der Parameter $a$ ist in beiden Formen der Streckfaktor ($|a|>1$) oder der Stauchfaktor ($|a|<1$). Die Parameter $d$ und $e$ in der Scheitelpunktform sind die Koordinaten des Scheitelpunktes $S(d|e)$. An diesen kann abgelesen werden, wie die Parabel verschoben wird.

Betrachten wir die Normalparabel zu $f(x)=x^2$. Hier ist $a=1$ und $d=e=0$. Diese ist in dem Bild blau eingezeichnet.

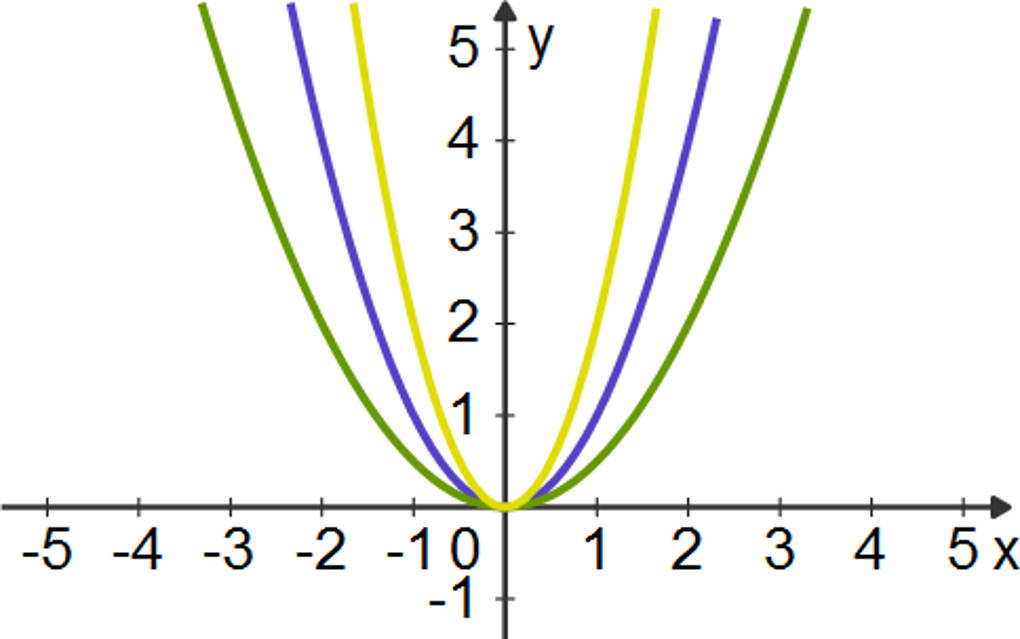
• Für $a>0$ ($a<0$) ist die Parabel nach oben (unten) geöffnet.
• Für $|a|>1$ wird die Parabel gestreckt. Anschaulich bedeutet dies, dass die Parabel enger ist als die Normalparabel. Dies ist in dem obigen Bild die gelbe Parabel.
• Für $|a|<1$ wird die Parabel gestaucht. Das bedeutet, dass die Parabel weiter ist als die Normalparabel. Dies ist in dem obigen Bild die grüne Parabel.

Der Scheitelpunkt einer nach oben (unten) geöffneten Parabel ist deren tiefster (höchster) Punkt. Durch den Scheitelpunkt verläuft die vertikale Symmetrieachse der Parabel.

• Sei $d>0$ ($d<0$), dann ist die Parabel entlang der x-Achse nach rechts (links) verschoben.
• Wenn $e>0$ ($e<0$) ist, ist die Parabel entlang der y-Achse nach oben (unten) verschoben.

Eponentialfunktionen

Betrachten wir nun die Exponentialfunktion genauer.

$f(x)=a\cdot 2^{c(x-d)}+e$

• Ist der Parameter $a<0$, führt dies zu einer Spiegelung an der x-Achse.
• Ist $|a|>1$ ($|a|<1$), wird der Graph der Funktion entlang der y-Achse gestreckt (gestaucht).
• Ist der Parameter $c<0$, führt dies zu einer Spiegelung an der y-Achse.
• $|c|>1$ ($|c|<1$) führt zu einer Streckung (Stauchung) des Funktionsgraphen entlang der x-Achse.
• $d>0$ ($d<0$) führt zu einer Verschiebung des Funktionsgraphen entlang der x-Achse nach rechts (links).
• Für $e>0$ ($e<0$) wird der Funktionsgraph entlang der y-Achse nach oben (unten) verschoben.

Du erkennst bereits, dass die Auswirkung der Parameter auf Funktionsgraphen recht ähnlich ist.

Sei nun auch die Basis $b>0$ der Funktion $f(x)=b^x$ frei wählbar:

• Für $0<b<1$ ist="" der="" graph="" exponentialfunktion="" an="" y-achse="" gespiegelt.="" monoton="" fallend.="" *="" für="" $b="1$" die="" funktion="" konstant.="" verläuft="" parallel="" zur="" x-achse.="" ###="" trigonometrische="" funktionen="" zuletzt="" schauen="" wir="" uns="" den="" einfluss="" von="" parametern="" auf="" trigonometrische="" funktionen="" am="" beispiel="" allgemeinen="" sinusfunktion="" $f(x)="a\cdot" \sin(bx-d)+e$="" an.="" wertebereich="" sinusfunktion="" $\mathbb{d}_f="[-1;1]$." länge="" dieses="" intervalls,="" also="" abstand="" zwischen="" maximalem="" und="" minimalem="" funktionswert,="" wird="" als="" amplitude="" bezeichnet.="" funktionswerte="" wiederholen="" sich.="" es="" gilt="" $f(x+2\pi)="f(x)$." $2\pi$-periodisch.="" in="" abhängigkeit="" dem="" parameter="" $a$="" ändert="" sich="" amplitude="" $b$="" periode.="" $|b|="">1$ ($|b|<1$) verkleinert (vergrößert) sich die Periode zu $\frac{2\pi}{|c|}$. $b<0$ bewirkt eine Spiegelung des Funktionsgraphen an der y-Achse.
• Der Parameter $d$ bewirkt wie bei den quadratischen Funktionen und den Exponentialfunktionen eine Verschiebung entlang der x-Achse. Der Parameter $d$ hat keine Auswirkung auf die Amplitude oder Periode.
• Der Parameter $e$ bewirkt eine Verschiebung entlang der y-Achse. Auch der Parameter $e$ hat keine Auswirkung auf die Amplitude oder Periode.
• $a<0$ bewirkt eine Spiegelung des Funktionsgraphen an der x-Achse. Für $|a|>1$ ($|a|<1$) vergrößert (verkleinert) sich die Amplitude um den Faktor $|a|$.</b<1$>