Sinusfunktion
Ankathete, Gegenkathete, Hypotenuse, Verhältnis, Bogenmaß, DEG, RAD, GRAD, trigonometrische Funktionen
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Die Definition des Sinus in einem rechtwinkligen Dreieck.
- Die Sinusfunktion am Einheitskreis
- Das Bogenmaß
Die Definition des Sinus in einem rechtwinkligen Dreieck.
Der Sinuswert eines spitzen Winkels in einem rechtwinkligen Dreieck ist der Quotient aus der Länge der Gegenkathete dieses Winkels sowie der der Hypotenuse.
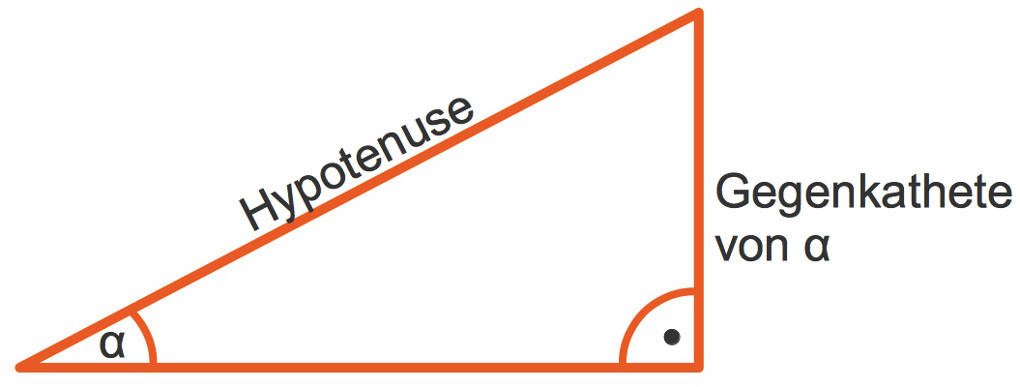
Darüber hinaus sind der Cosinuswert sowie der Tangenswert eines spitzen Winkels in einem rechtwinkligen Dreieck wie folgt erklärt:
$\sin(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}}$
$\cos(\alpha)=\frac{\text{Ankathete von }\alpha}{\text{Hypotenuse}}$
$\tan(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha}$
Die Sinusfunktion wird ebenso wie die Cosinus- und Tangensfunktion als trigonometrische Funktion bezeichnet. Diese Funktionen sind nicht nur in rechtwinkligen Dreiecken erklärt und auch nicht nur für spitze Winkel.
Die Sinusfunktion am Einheitskreis
Die trigonometrischen Funktionen können mithilfe des Einheitskreises dargestellt und auch erklärt werden.
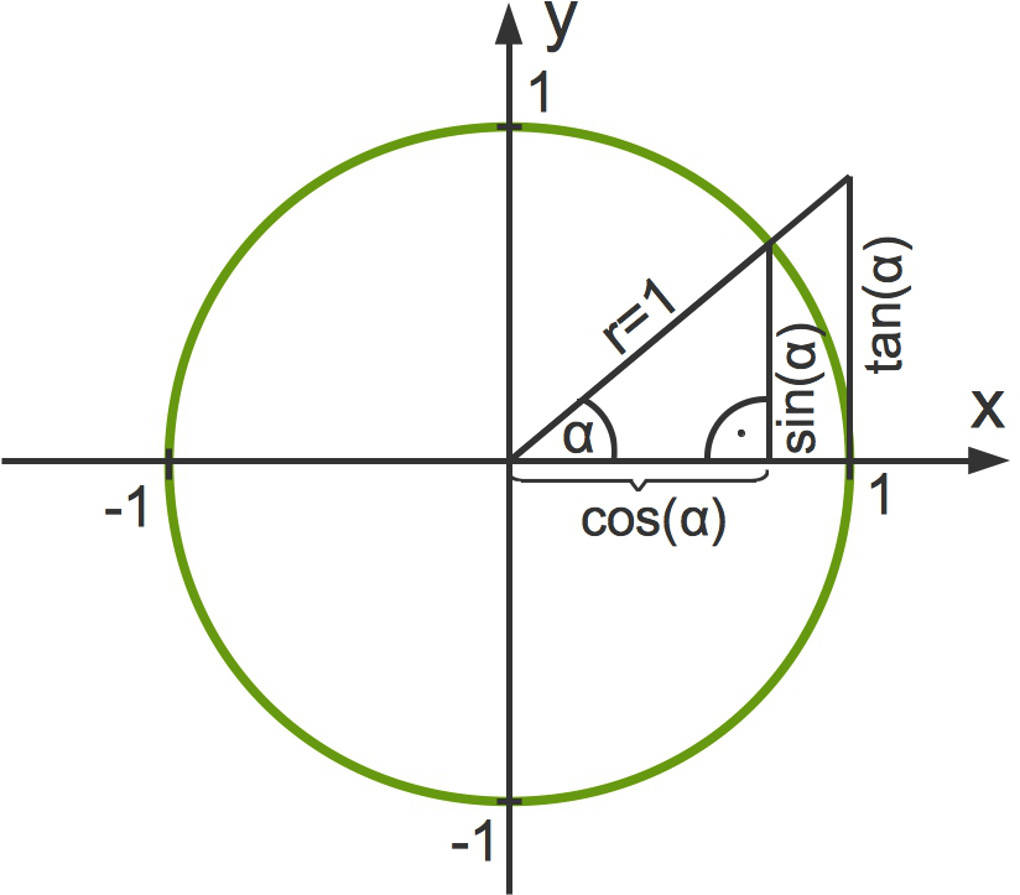
Der Einheitskreis ist ein Kreis mit dem Radius $r=1$. Du kannst hier ein rechtwinkliges Dreieck sehen. Die Hypotenuse ist der Radius. Damit ist der Sinus des Winkels $\alpha$ die Länge der Gegenkathete.
Nun kann man sich klarmachen, wie der Sinuswert des Winkels $\alpha$ sich verändert, wenn der Winkel verändert wird.
- Wenn $\alpha=0^\circ$ ist, dann ist $\sin(\alpha)=0$.
- Wenn $\alpha=90^\circ$ ist, dann ist $\sin(\alpha)=1$.
- Wenn $\alpha=180^\circ$ ist, dann ist $\sin(\alpha)=0$.
- Wenn $\alpha=270^\circ$ ist, dann ist $\sin(\alpha)=-1$.
- $\alpha=360^\circ$ entspricht dem Winkel $\alpha=0^\circ$.
Da nun das Abschreiten des Kreises erneut beginnt, wiederholen sich die Sinuswerte periodisch.
Die Sinuswerte können vom Einheitskreis in ein x-y-Koordinatensystem übertragen werden.
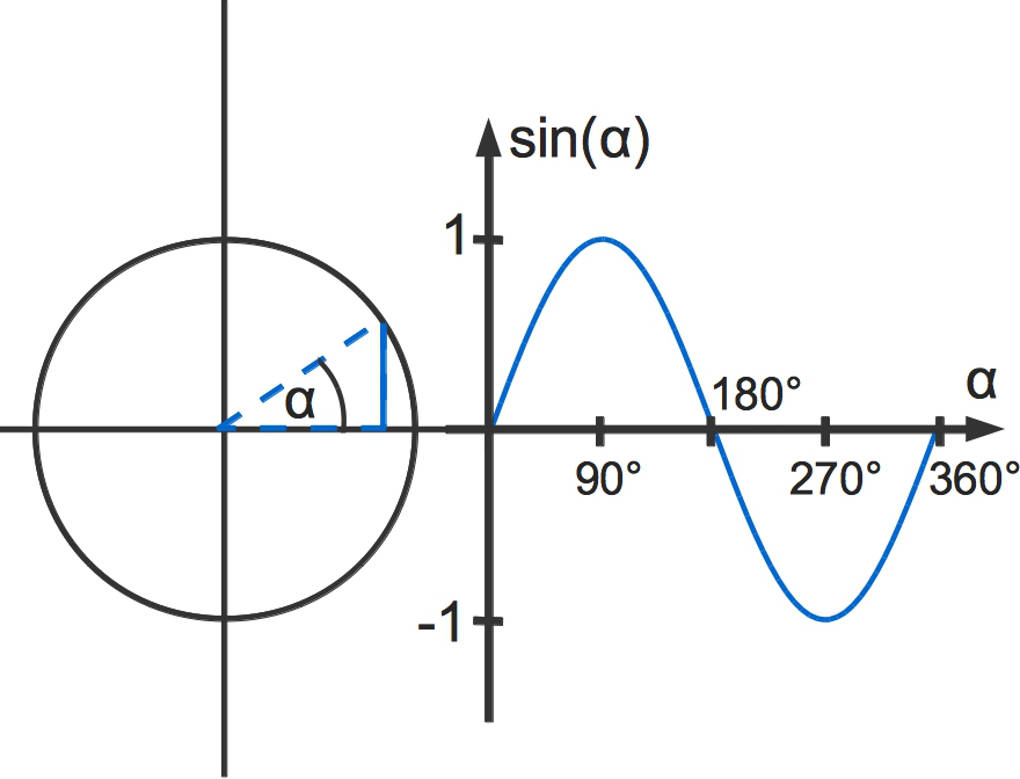
Die Sinusfunktion hat die folgenden Eigenschaften:
- Sie ist für alle reellen Werte definiert $\mathbb{D}=\mathbb{R}$.
- Ihr Wertebereich ist gegeben durch $\mathbb{W}=[-1;1]$.
- Ab $360^\circ$ wiederholt sich der Verlauf. Dies wird als Periodizität bezeichnet. Die Periodenlänge beträgt $360^\circ$. Du kannst dir das so vorstellen: Du kopierst den Graph der Funktion für $\alpha\in[0^\circ;360^\circ]$ und fügst diese Kopie links von $0^\circ$ und rechts von $360^\circ$ beliebig oft an.
- Die Nullstellen der Sinusfunktion sind die ganzzahligen Vielfachen von $180^\circ$. Das bedeutet: Für $\alpha=k\cdot 180^\circ;~k\in \mathbb{Z}$ gilt $\sin(\alpha)=0$.
- Der Graph der Sinusfunktion ist punktsymmetrisch zum Koordinatenursprung. Darüber hinaus ist er punktsymmetrisch zu jedem Nullpunkt der Funktion.
- Wenn du eine Parallele zur y-Achse durch eine beliebigen Hoch- oder Tiefpunkt der Funktion zeichnest, so ist der Graph der Sinusfunktion achsensymmetrisch zu dieser Parallelen.
- Der Abstand von dem höchsten zu dem niedrigsten Wert der Sinusfunktion wird als Amplitude der Funktion bezeichnet. Diese ist $1-(-1)=2$.
Das Bogenmaß
Zur Berechnung von Sinuswerten verwendest du den Taschenrechner.

Du musst dabei etwas beachten:
Wenn mit den trigonometrischen Funktionen gerechnet wird, kann das Winkelmaß, so wie oben zu sehen, verwendet werden. An Stelle vom Winkelmaß kann auch mit dem Bogenmaß gerechnet werden.
Je nachdem, mit welchem der beiden Maße gerechnet wird, wird der Taschenrechner verschieden eingestellt:
- auf DEG für „degree“, also Winkelmaß, oder
- auf RAD für „radius“, also Bogenmaß.
Stelle dir wieder den Einheitskreis vor.

Zu jedem Winkel, im Winkelmaß $^\circ$, gehört ein Kreisbogen, im Bogenmaß. Dieser Bogen ist hier mit $b$ bezeichnet. Die Maßeinheit ist ein Längenmaß, zum Beispiel $cm$ oder $dm$.
Umrechnung von Winkelmaß in Bogenmaß
Sei der Winkel $\alpha$ gegeben, dann ist das Verhältnis dieses Winkels zu dem gesamten Winkel ebenso groß wie das des zugehörigen Bogens zu dem Gesamtumfang des Einheitskreis $2~\pi$.
$\frac{\alpha}{360^\circ}=\frac{b}{2~\pi}$
Die Multiplikation mit $2~\pi$ führt zu:
$b=\frac{\alpha}{360^\circ}\cdot 2~\pi$.
Beispiele:
- Der Winkel $\alpha=0^\circ$ entspricht dem Bogenmaß $b=0$.
- Der Winkel $\alpha=90^\circ$ entspricht dem Bogenmaß $b=\frac{\pi}2$.
- Der Winkel $\alpha=180^\circ$ entspricht dem Bogenmaß $b=\pi$.
Damit können einige der oben bereits genannten Eigenschaften auch mit Hilfe des Bogenmaßes ausgedrückt werden. Alle $2~\pi$ wiederholt sich der Verlauf der Sinusfunktion. Dies wird als $2~\pi$-Periodizität bezeichnet. Zudem sind die Nullstellen der Sinusfunktion ganzzahlige Vielfache von $\pi$. Das bedeutet, für $x=k\cdot \pi;~k\in \mathbb{Z}$ gilt $\sin(x)=0$.
Umrechnung von Bogenmaß in Winkelmaß
Sei nun das Bogenmaß $b$ gegeben. Es gilt wiederum:
$\frac{\alpha}{360^\circ}=\frac{b}{2~\pi}$.
Die Multiplikation mit $360^\circ$ resultiert in:
$\alpha=\frac{b}{2~\pi}\cdot 360^\circ$.
Alle Videos zum Thema
Videos zum Thema
Sinusfunktion (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Sinusfunktion (8 Arbeitsblätter)
-
 Sinusfunktion – Überblick und Eigenschaften
PDF anzeigen
Sinusfunktion – Überblick und Eigenschaften
PDF anzeigen -
 Parameter bei der Sinusfunktion
PDF anzeigen
Parameter bei der Sinusfunktion
PDF anzeigen -
 Cosinusfunktion – Überblick
PDF anzeigen
Cosinusfunktion – Überblick
PDF anzeigen -
 Parameter a bei der Sinusfunktion
PDF anzeigen
Parameter a bei der Sinusfunktion
PDF anzeigen -
 Parameter b bei der Sinusfunktion
PDF anzeigen
Parameter b bei der Sinusfunktion
PDF anzeigen -
 Parameter d bei der Sinusfunktion
PDF anzeigen
Parameter d bei der Sinusfunktion
PDF anzeigen -
 Parameter e bei der Sinusfunktion
PDF anzeigen
Parameter e bei der Sinusfunktion
PDF anzeigen -
 Winkelfunktionen – spezielle Funktionswerte
PDF anzeigen
Winkelfunktionen – spezielle Funktionswerte
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter





















