Normalverteilung
Standardnormalverteilung, sigma, mü, Mittelwert, Abweichung, 3 sigma Regel, Tabelle
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Standardisierung der Binomialverteilung
Die Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Dabei wird jedem $k$ die Wahrscheinlichkeit $P(X=k)$ durch die Formel von Bernoulli zugeordnet:
$P(X=k)=B_{n;p}(k)=\begin{pmatrix} n \\ k \end{pmatrix}\cdot p^k\cdot (1-p)^{n-k}$
Die Variablen $n$, $p$, $k$ haben folgende Bedeutung:
- $n$ ist die Länge der Bernoullikette, also die Anzahl der Durchführungen des Experimentes.
- $p$ ist die Trefferwahrscheinlichkeit und
- $k$ ist die Anzahl der Treffer eines mehrstufigen Bernoulli-Experimentes
Hier siehst du die Binomialverteilung für $p=0,2$ und $n=10$.

Um Punktwahrscheinlichkeiten $P(X=k)$ zu erhalten, kannst du Tabellen verwenden. Diese Tabellen gehen aber oftmals nur bis $n=100$. Wie können also Wahrscheinlichkeiten berechnet werden, wenn $n$ größer wird?
Möchtest du Intervallwahrscheinlichkeiten $k_1 < p < k_2$ für hohe $n$ berechnen, wirst du keine geeigneten Tabellen finden.
An dieser Stelle kommt die Normalverteilung ins Spiel, die durch die Standardisierung der Binomialverteilung zustande kommt.
Normalverteilung
Die Normalverteilung ist eine stetige Wahrscheinlichkeitsverteilung. Sie wird nach ihrem Entdecker auch als Gauß-Verteilung bezeichnet.

Carl-Friedrich Gauß (geb. 30. April 1777, gest. 23. Februar 1855) war ein bedeutender deutscher Mathematiker. Er wurde bereits zu Lebzeiten als Fürst der Mathematik bezeichnet. Auf ihn geht unter anderem die Gauß-Funktion oder (Gauß'sche) Glockenkurve zurück, welche sich auf dem letzten 10 DM Schein befand.
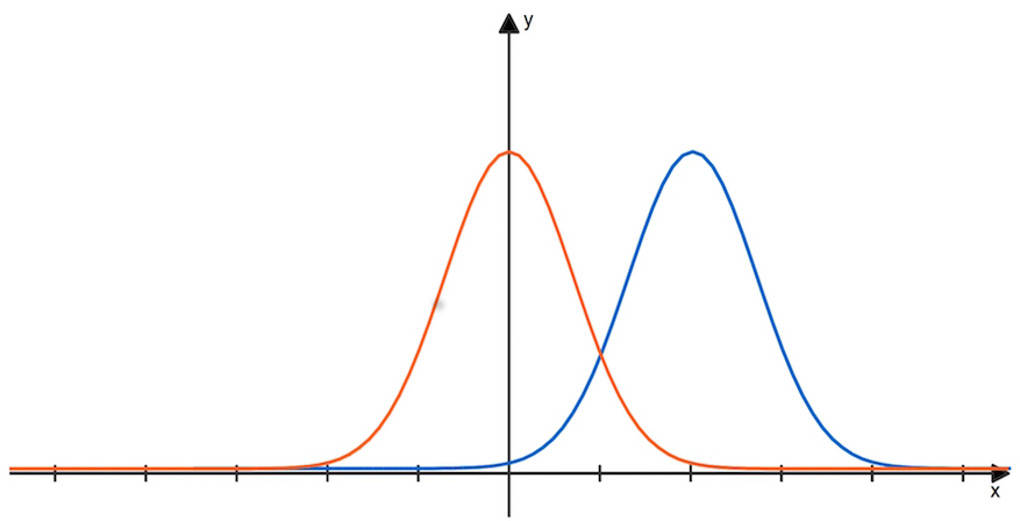
Die blaue Kurve zeigt die zur Normalverteilung gehörende Dichtefunktion. Du kannst sicherlich die Ähnlichkeit zur obigen Binomialverteilung erkennen. Deren Dichtefunktion ist gegeben durch:
$\large{\psi(x)=\frac1{\sigma\sqrt{2\pi}}\cdot e^{-0,5\left(\frac{x-\mu}{\sigma}\right)^2}}$
Zu der zugehörigen Verteilungsfunktion, der Gauß-Funktion, gelangst du durch Integration:
$\large{\phi(x)=\frac1{\sigma\sqrt{2\pi}}~\int\limits_{-\infty}^{x} e^{-0,5\left(\frac{t-\mu}{\sigma}\right)^2}dt}$
Für $\mu=0$ und $\sigma=1$ erhältst du die Standardnormalverteilung, welche so wie die rote Kurve aussehen könnte.
Die Parameter der Normalverteilung
Die Parameter der Normalverteilung sind $\mu$, $\sigma$ und $\sigma ^2$:
- Der Erwartungswert $\mu=n \cdot p$ beschreibt die Stelle, an welcher die Dichtefunktion ihren höchsten Wert annimmt.
- Die Standardabweichung $\sigma= \sqrt{n \cdot p \cdot (1-p)}$ sowie die Varianz $\sigma ^2$ sind Maße für die Streuung der Verteilung.
Schauen wir uns hierzu ein Beispiel an.
Beispiel
Du würfelst mit einem Würfel $n=120$ mal. Du möchtest wissen, wie groß die Wahrscheinlichkeit ist, $k=20$ mal eine $6$ zu würfeln. Diese Wahrscheinlichkeit kann auch mit der Formel von Bernoulli berechnet werden. Um diese Wahrscheinlichkeit mithilfe der Normalverteilung anzunähern, benötigst du den Erwartungswert $\mu$ sowie die Standardabweichung $\sigma$.
- $p=\frac16$
- $\mu=n \cdot p = 120\cdot \frac16=20$ und
- $\sigma =\sqrt{n \cdot p \cdot (1-p)} = \sqrt{120\cdot \frac16\cdot \frac56}\approx 4,08$
Bevor nun die Wahrscheinlichkeit mithilfe der Verteilungsfunktion näherungsweise berechnet werden kann, muss die Laplace-Bedingung überprüft werden: Die Standardabweichung muss größer als $3$ sein.
$\sigma=\sqrt{120\cdot \frac16\cdot\frac56}\approx 4,08 >3~\surd$
Da dies hier der Fall ist, kann nun die Wahrscheinlichkeit berechnet werden:
$B_{n;p}(20)\approx \psi(20)=\frac1{4,09\sqrt{2\pi}}\cdot e^{-0,5\left(\frac{20-20}{4,09}\right)^2}\approx 0,0389$
Dabei können wir diese Beobachtungen machen: Je größer $n$ ist,
- desto größer wird die Standardabweichung.
- umso mehr nähert sich die Binomialverteilung der Normalverteilung an.
- umso besser kann die gesuchte Wahrscheinlichkeit angenähert werden.
Sigma-Regeln
Wir können Aussagen über die Wahrscheinlichkeitsverteilung treffen, wenn wir den Erwartungswert $\mu$ und die Standardabweichung $\sigma>3$ einer Normalverteilung kennen. Hierfür gibt es die Sigma-Regeln. Diese geben Abschätzungen für Intervallwahrscheinlichkeiten an.
- 1-$\sigma$ - Regel: $P(\mu-1\cdot \sigma\le X \le \mu+1\cdot\sigma)\approx 0,680$
- 2-$\sigma$ - Regel: $P(\mu-2\cdot \sigma\le X \le \mu+2\cdot\sigma)\approx 0,955$
- 3-$\sigma$ - Regel: $P(\mu-3\cdot \sigma\le X \le \mu+3\cdot\sigma)\approx 0,997$
Fassen wir dies einmal in Worte: Stellen wir uns die Dichtefunktion einer Wahrscheinlichkeitsverteilung vor.
- Wenn wir nun, vom Erwartungswert ausgehend, eine Standardabweichung $\sigma$ nach links und eine nach rechts gehen, haben wir damit $68~\%$ der möglichen Ergebnisse abgedeckt.
- Gehen wir zwei Standardabweichung $\sigma$ nach links und rechts, so befinden sich in diesem Intervall $95,5~\%$ der möglichen Ergebnisse.
Alle Videos zum Thema
Videos zum Thema
Normalverteilung (7 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Normalverteilung (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal












 Normalverteilung – Standardisierung der Binomialverteilung
Normalverteilung – Standardisierung der Binomialverteilung
 Normalverteilung – Gaußsche Glockenkurve und Laplace-Bedingung
Normalverteilung – Gaußsche Glockenkurve und Laplace-Bedingung
 Normalverteilung – Anwendung der Näherungsformeln
Normalverteilung – Anwendung der Näherungsformeln









